Didáctica de las transformaciones lineales: entre la abstracción matemática y la enseñanza significativa

Marcos Iván Vilchez Ruiz
Universidad Nacional Autónoma de Nicaragua. Centro Universitario Regional de Estelí. UNAN-Managua/CUR-Estelí, Nicaragua.
https://orcid.org/0009-0002-7536-9286
marcosvilchezruiz@gmail.com

Francis Judith Centeno Centeno
Universidad Nacional Autónoma de Nicaragua. Centro Universitario Regional de Estelí. UNAN-Managua/CUR-Estelí, Nicaragua.
https://orcid.org/0009-0005-4710-5920
franjudithcenteno@gmail.com

Deyvid Francisco Rivera Rivera
Universidad Nacional Autónoma de Nicaragua. Centro Universitario Regional de Estelí. UNAN-Managua/CUR-Estelí, Nicaragua.
https://orcid.org/0009-0000-5284-1598
riveradeyvid406@gmail.com

Flor Ibeth Calero Torrez
Universidad Nacional Autónoma de Nicaragua. Centro Universitario Regional de Estelí. UNAN-Managua/CUR-Estelí, Nicaragua.
https://orcid.org/0009-0004-7056-8336
floricalero99@gmail.com

Samantha Lucia Cruz López
Universidad Nacional Autónoma de Nicaragua. Centro Universitario Regional de Estelí. UNAN-Managua/CUR-Estelí, Nicaragua.
https://orcid.org/0000-0003-2340-6532
samlucruz16@gmail.com

 

RECIBIDO

26/05/2025

ACEPTADO

02/07/2025

 

 

INTRODUCCIÓN

 

La enseñanza de las transformaciones lineales representa uno de los mayores desafíos en la educación matemática universitaria, en especial en cursos de álgebra lineal son funciones que se estudian en álgebra lineal. “Son funciones entre espacios vectoriales que conservan la estructura lineal de cada espacio” Universidad de Buenos Aires (2020). Su naturaleza profundamente abstracta, cimentada en conceptos teóricos como espacios vectoriales, matrices y funciones lineales, contrasta con la necesidad de brindar experiencias significativas que permitan a los estudiantes construir conocimientos duraderos y transferibles pues según Hulatt & Freitas (2019) la transformación lineal no está ligada a ejemplos específicos, sino que define una estructura general que puede aplicarse a cualquier espacio vectorial. Esto la convierte en un concepto abstracto que es fundamental en el álgebra línea. Este ensayo explora cómo equilibrar la formalidad matemática con estrategias didácticas orientadas al aprendizaje comprensivo y contextualizado.

El presente texto tiene como objetivo principal analizar la didáctica de las transformaciones lineales desde una perspectiva que articule rigurosidad formal y relevancia pedagógica. Para ello, se desarrollarán diversos subtemas:

• La definición formal de transformación lineal y sus propiedades
• la representación matricial y su interpretación geométrica
• la importancia de los subespacios invariante
• la relación con el cambio de base
• la integración de recursos didácticos

El uso de software matemático y la resolución de problemas contextualizados. Cada sección ofrecerá tanto el contenido matemático como propuestas didácticas para facilitar su enseñanza.

Desarrollo del tema

• Fundamentos matemáticos de las transformaciones lineales

1.1 Definición formal y propiedades fundamentales
En matemáticas, una transformación lineal es una función entre dos espacios vectoriales como dice Pustilnik (2016) “por ser función, tiene su dominio y su codominio” que conserva las operaciones de suma vectorial y multiplicación escalar. Formalmente, dada una aplicación T : V entre espacios vectoriales sobre un cuerpo K, se dice que es lineal si para todo u, v y todo c se cumple:

 

T(u+v) -T(u)+t(v),     T(cu)-cT(u) (1)

 

Estas propiedades garantizan que la estructura algebraica del espacio original se preserve bajo la transformación. Esta definición puede resultar abstracta para estudiantes sin experiencia en teoría de estructuras algebraicas, por lo cual es crucial introducirla gradualmente, iniciando con ejemplos concretos en y , donde es posible visualizar y manipular vectores gráficamente (Herrera-Castrillo, 2024).

El estudio de las propiedades de las transformaciones lineales incluye conceptos como el núcleo (ker) y la imagen (im) de una transformación, los cuales son subespacios de V y W respectivamente. El teorema fundamental del álgebra lineal establece que:

 

Dim(ker(T))+dim(im(T))-dim(V) (2)

 

Esta igualdad, conocida como el teorema del rango-nulidad, es esencial para comprender la estructura interna de una transformación y permite una introducción natural a conceptos como inyectividad, sobreyectividad y biyección en el contexto lineal.

Figura 1. Visualización del efecto de una transformación lineal sobre vectores: conservación del origen, suma y multiplicación escalar.

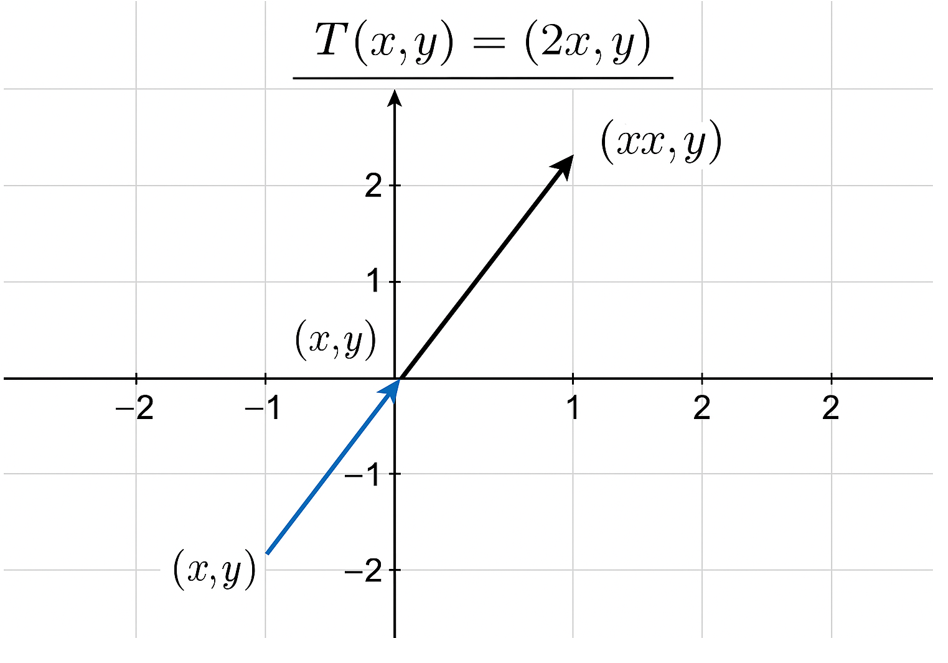
Nota. Mostrar cómo vectores cambian bajo (T), preservando el origen, suma y multiplicación escalar. Fuente: Elaboración propia

Representación matricial de las transformaciones lineales

Una de las herramientas más potentes para el estudio de las transformaciones lineales es su representación matricial según menciona Scala Learning (2018). Dado un espacio vectorial V de dimensión n con base {v₁, ….. v_n } toda transformación lineal T: V puede representarse mediante una matriz A tal que:

 

T(x)-Ax (3)

 

donde x es el vector columna que representa a un vector v en la base elegida. Esta representación facilita la aplicación de técnicas computacionales y permite analizar el comportamiento de T mediante operaciones matriciales como la determinación del rango, la inversibilidad, y la diagonalización.

Desde el punto de vista didáctico, es altamente recomendable introducir la representación matricial junto con visualizaciones gráficas en y , donde es posible ver cómo vectores base se transforman mediante rotaciones, escalados, reflexiones, etc. Herramientas como GeoGebra, Desmos 3D o Python (mediante librerías como Matplotlib y NumPy) pueden enriquecer la comprensión y fomentar el aprendizaje activo (Herrera Castrillo & López, 2025).

Figura 2. Representación gráfica de una matriz actuando sobre la base canónica: rotación, reflexión o proyección.

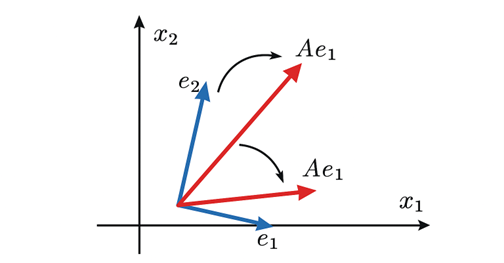
Nota. Visualización de la acción de una matriz (A) sobre una base canónica, como rotación o proyección. Fuente: Elaboración propia

Geometría de las transformaciones lineales

Interpretación geométrica en y

Toda transformación lineal en y  puede interpretarse geométricamente como una operación que modifica la forma, es decir, según Universidad de Harvard (2023) “Una transformación lineal es una operación que respeta la suma, la multiplicación y el 0”, orientación o escala de los objetos, sin alterar la linealidad de los mismos. Ejemplos comunes incluyen rotaciones, reflexiones, proyecciones y estiramientos (Herrera Castrillo & López, 2025). Por ejemplo, la matriz:

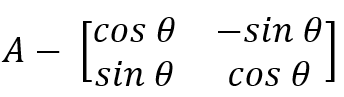(4)

representa una rotación de radianes alrededor del origen en . Estas representaciones permiten al estudiante vincular el concepto abstracto de matriz con transformaciones visuales tangibles, facilitando la construcción de significado.

En el aula, es clave fomentar la exploración de estas transformaciones mediante software interactivo. Por ejemplo, se puede pedir al estudiante que modifique los coeficientes de una matriz y observe cómo cambia la transformación en tiempo real, reforzando así el vínculo entre forma algebraica y consecuencia geométrica.

Subespacios invariantes y valores propios

Un concepto central en la geometría de las transformaciones lineales es el de subespacio invariante Mohamed (2020) “El método del subespacio invariante (ISM) es un método eficaz para resolver ecuaciones diferenciales parciales fraccionarias”. Un subespacio U  V es invariante bajo T si T(u) para todo u . En particular, los vectores propios (o eigenvectores) de una transformación son aquellos que permanecen en su misma línea de acción, es decir, que satisfacen:

 

T(v) - v (5)

 

Donde  es un escalar llamado valor propio. El estudio de valores y vectores propios permite descomponer la acción de una transformación en direcciones privilegiadas, siendo esencial para procesos como la diagonalización y la reducción de matrices.

Desde una perspectiva didáctica, los valores propios pueden presentarse inicialmente como direcciones que no cambian su sentido, aunque sí su magnitud, bajo una transformación. Con ayuda de simuladores y ejercicios visuales, se puede inducir al estudiante a descubrir estos valores como soluciones de la ecuación:

 

det(A-) – 0 (6)

 

lo cual introduce también al estudiante en la resolución de polinomios característicos y la importancia de los determinantes.

Figura 3. Visualización del comportamiento de los eigenvectores bajo una transformación lineal: dirección invariante.

 

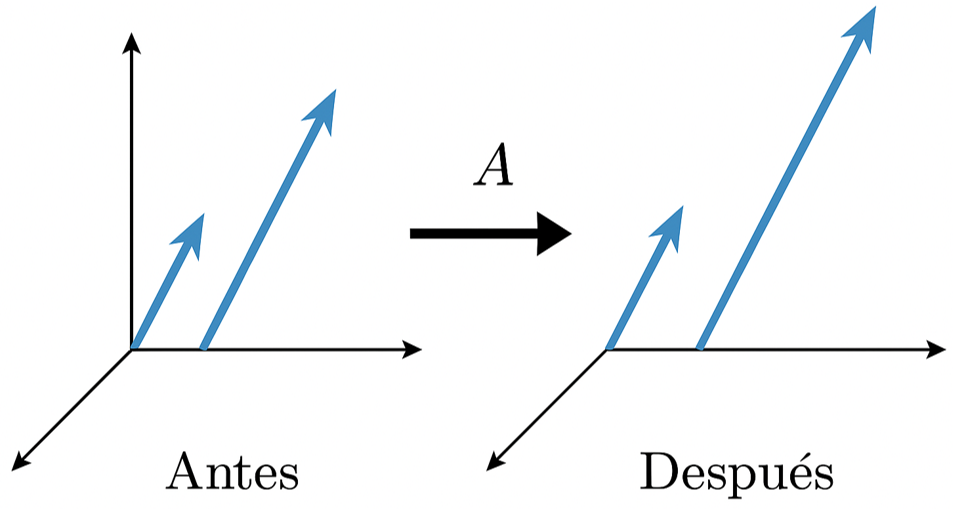
Nota. Visualiza cómo los eigenvectores se mantienen en su dirección. Fuente: Elaboración propia

Cambio de base y diagonalización

Transformaciones bajo distintas bases

Una misma transformación lineal puede tener distintas representaciones matriciales dependiendo de la base elegida. Universidad de Guanajuato (2021) “Para obtener la representación matricial de una transformación lineal, se aplica la transformación a los vectores base del espacio vectorial original. “ Si T:V es una transformación lineal y B y  son dos bases de V, entonces las matrices y están relacionadas por:

 

P (7)

 

Donde P es la matriz de cambio de base de B a . Esta relación forma la base del estudio de semejanza de matrices y es fundamental en teoría espectral.
Desde el punto de vista pedagógico, este concepto puede explorarse como un puente entre la perspectiva algebraica y la geométrica: cambiar la base es como cambiar el sistema de coordenadas, según Secretaria de Educación Pública [SEP] (2025) “La geometría analítica asocia pares de números a puntos y ecuaciones a curvas”. De esta forma, una representación complicada en una base puede transformarse en una forma más simple (por ejemplo, una matriz diagonal) al elegir una base adecuada.

Diagonalización y su significado didáctico

Una matriz A es diagonalizable si existe una base de  formada por vectores propios de A. Universidad de Jaén (2023) “El proceso de cálculo de la matriz diagonal y de la matriz de paso se denomina diagonalización de A”. En este caso, A es semejante a una matriz diagonal D, es decir:

 

(8)

 

Esta propiedad permite simplificar potencias de matrices, resolver sistemas de ecuaciones diferenciales y comprender la dinámica de sistemas lineales. El proceso de diagonalización revela la estructura interna de una transformación y sus "ejes naturales" de acción.

Desde lo didáctico, la diagonalización puede introducirse como una técnica de simplificación: al transformar una matriz compleja en una diagonal, se facilita el cálculo y se clarifica el efecto de la transformación sobre los vectores. Es importante presentar ejemplos en los que se observe claramente cómo los vectores propios estiran o comprimen el espacio sin rotarlo “Facilita el cálculo de potencias, exponenciales y sistemas de ecuaciones diferenciales” (Fiveable, 2018).

 

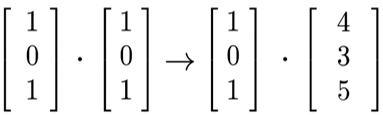(9)

 

Muestra visualmente el “alineamiento” de la transformación con los ejes.

Didáctica y recursos para la enseñanza significativa

Enfoques pedagógicos y teorías del aprendizaje

La enseñanza de las transformaciones lineales requiere más que exposiciones teóricas. Desde la perspectiva del constructivismo, los estudiantes deben construir activamente su conocimiento a partir de experiencias significativas como afirma Parreño (2019)  “el constructivismo es una corriente de aprendizaje que propone que los estudiantes construyen su conocimiento de forma activa”. Las teorías de Vygotsky, Ausubel y Piaget apoyan la importancia del aprendizaje significativo.
En este sentido, es vital articular la abstracción matemática con aplicaciones reales o semi-realistas, explorando contextos como la computación gráfica, la economía o la física. Problemas contextualizados permiten al estudiante ver la utilidad de las transformaciones lineales y fomentan una actitud positiva hacia el aprendizaje matemático.

Recursos digitales y representaciones múltiples

El uso de tecnología educativa transforma la manera en que se puede enseñar álgebra lineal. Software como GeoGebra 3D, MATLAB, Python o Wolfram Mathematica permite experimentar con transformaciones en tiempo real, ya que “los estudiantes pueden acceder a una gran cantidad de información y recursos educativos en línea.” Reyes (2024) Y así explorar visualizaciones tridimensionales e incluso resolver problemas simbólicos.

 

CONCLUSIONES

La enseñanza de las transformaciones lineales es un equilibrio entre la belleza formal de la teoría matemática y la necesidad de que sea significativa para el estudiante. Entender las transformaciones como funciones estructuradas que modelan fenómenos y pueden visualizarse, procesarse y aplicarse en diferentes contextos es la clave para lograr un aprendizaje profundo.

Para lograrlo es necesario combinar diferentes enfoques:

• Partir de ejemplos concretos
• Avanzar hacia la abstracción
• Utilizar tecnologías educativas
• Aplicar los conocimientos en contextos reales
• Desarrollar el pensamiento crítico.

De esta forma, las transformaciones lineales dejan de ser un conjunto de definiciones abstractas y se convierten en poderosas herramientas de modelado y análisis.
Este artículo intenta ofrecer una visión del tema, mostrando que las transformaciones lineales pueden enseñarse de forma consistente sin perder su claridad y utilidad. Quedan direcciones abiertas para la investigación sobre estrategias de evaluación específicas, desarrollo curricular y formación docente en esta área crítica de la educación matemática.

 

REFERENCIAS BIBLIOGRÁFICAS