Los problemas de comprensión del álgebra en estudiantes universitarios
William Oswaldo Flores López1
Elena Auzmendi Escribano2
Resumen
Este artículo es resultado de investigaciones en torno a los problemas asociados a la comprensión del álgebra que presentan estudiantes universitarios en la construcción del conocimiento matemático, tomando en consideración los obstáculos cognitivos, la familia de dificultades asociadas al álgebra y errores procedimentales de los estudiantes universitarios en el álgebra. En el desarrollo de la ponencia se describirá a partir del análisis hermenéutico, algunos supuestos básicos del papel que juegan los sentimientos y emociones en las matemáticas y los procesos de matematización.
Palabras Clave: comprensión del álgebra; educación superior; errores procedimentales; obstáculos cognitivos.
Summary
This article is the result of researches related to problems associated with the comprehension of algebra by university students in the construction of mathematical knowledge, taking into account cognitive obstacles, the family of difficulties associated with algebra and the procedural errors of the university students with this subject. The development of the paper will be described based on a hermeneutic analysis, some basic assumptions of the role that the feelings and emotions holds in mathematics, as well as the mathematization processes.
Keywords: understanding of algebra; higher education; procedural errors; cognitive obstacles.
I. Introducción
La importancia que tiene la noción de comprensión para la didáctica de las matemáticas se ve plasmada en diferentes investigaciones y documentos curriculares de amplia difusión internacional como en NCTM (2000), TIMSS (2003), OECD (2004), y señalan que los estudiantes deberían de comprender las matemáticas; sin embargo, la realidad del aula parece distanciarse de estos planteamientos. La práctica del aula parece decantarse hacia la práctica rutinaria de ejercicios algorítmicos, con clara predominancia del marco aritmético-algebraico, se promueve casi en exclusiva la comprensión instrumental (Skemp, 1976). Esta práctica muestra también debilidades, como la escasa puesta en escena de varios sistemas de representación del conocimiento matemático y la ausencia significativa de contextos y situaciones-problemas enfocados hacia la comprensión y consecuente aprendizaje, de los conceptos matemáticos objeto de estudio.
Consciente del escenario anterior, en esta comunicación nos centramos, en particular, en el análisis desde un punto de vista hermenéutico de los problemas asociados a la comprensión del álgebra. Todo ello, con la premisa que un estudiante comprende un determinado objeto matemático cuando lo usa competentemente en diferentes prácticas matemáticas (Godino & Batanero, 1994) y por ende tiene que adquirir la capacidad de pensar y razonar, argumentar y justificar, comunicar, modelar, representar, plantear y resolver problemas en matemáticas (OECD, 2005).
II. Desarrollo
Los problemas asociados al pensamiento algebraico
Los problemas asociados al pensamiento algebraico son estudiados en diferentes trabajos Kieran y Filloy (1989), Kieran (1992), Kaput (1999), Janvier (1987), Duval (1993), Chevallard, Bosch y Gascón (1997), Bolea, Bosch y Gascón (2001), Godino (2002), Godino, Batanero y Font (2007) y se tipifican de la siguiente manera:
Desde la perspectiva de la psicología cognitiva, Kieran y Filloy (1989) han identificado los factores que influyen sobre la enseñanza y aprendizaje del álgebra, que ponen de manifiesto las consecuencias de considerar el álgebra como aritmética generalizada. El enfoque lingüístico estudiado por Janvier (1987), Kaput (1999) y Duval (1993), consideran al lenguaje algebraico como el lenguaje básico de las matemáticas, centrado el interés en el estudio de los sistemas de representación semióticos que constatan la necesidad de aceptar que la apropiación de un objeto matemático difícilmente se logra sin la adquisición de diversas representaciones semióticas del mismo. Los estudios de Chevallard, Bosch y Gascón (1997), Bolea, Bosch y Gascón (2001), Godino (2002), Godino, Batanero y Font (2007), quienes realizan desde el enfoque antropológico y ontosemiótico, dichos estudios adoptan un punto de vista pragmático, centrado en el análisis del significado de los objetos matemáticos tanto a nivel institucional como personal, estudiando los fenómenos derivadas de la transposición didáctica escolar tratando de integrar los aspectos sintácticos, semánticos, pragmáticos y socioculturales.
Como problemas específicos del proceso Educativo del Álgebra se identifican los trabajados realizados por Brousseau (1983), Palarea y Socas (1994), Socas (1997), Kieran (1997), Pizón y Gallardo (2000), Vicario (2002) y Cajaraville et al. (2012), donde tratan de encontrar soluciones a preguntas como: ¿Qué pueden hacer y qué no pueden hacer los estudiantes en los niveles de comprensión del álgebra? Esta percepción se puede agrupar en los siguientes núcleos:
Los obstáculos epistemológicos y didácticos que constituyen una fuente de errores sistemáticos y persistentes que deben superarse para lograr nuevos aprendizajes (Brousseau, 1983). Palarea y Socas (1994) tipifica tres tipos de errores: (a) los que se originan por la existencia de obstáculos; (b) los errores del álgebra que están en la aritmética; y (c) los debidos a las características propias del lenguaje algebraico. También Socas (1997), puntualiza tres tipos de errores: (a) un obstáculo cognitivo; (b) ausencia de sentido de los sistemas de representación; y (c) actitudes afectivas y emocionales. En los estudios de Kieran (1997), se señala que en los problemas del álgebra elemental, en los que se presenta la variable como un valor desconocido que se debe localizar, las demandas conceptuales de los estudiantes se centran en: (1) comprender las letras como objeto que se usan para representar incógnitas, números generalizados y relaciones entre cantidades; (2) traducir los problemas a modelos algebraicos, basados en ecuaciones que representan las cantidades desconocidos y los otros datos del problema, según relaciones explicitas o implícitas en el enunciado de la tarea; y (3) resolver dichas ecuaciones. Estas demandas generan dificultades de aprendizaje en muchos estudiantes.
Otras problemas son mencionados en Pizón y Gallardo (2000) al intentar comprender: (a) la concatenación de términos algebraicos, en relación con la del sistema de numeración; (b) transformaciones entre números positivos y negativos en expresiones algebraicas; (c) inversión incorrecta de las operaciones (transposición de términos en una ecuación); (d) diferencia de la incógnita respecto a su coeficiente. Hay que destacar las aportaciones del estudio exploratorio de Vicario (2002) sobre las ideas asociadas a la variable con estudiantes de educación media y educación superior, muestran la escasa presencia de la idea de variable concebida como una magnitud, es decir, asociada a una representación geométrica (longitud, área, volumen). Se tiene una concepción de variable asociada a las letras y afloran concepciones alternativas en plano gráfico y conjuntista al plantear situaciones de variación; los estudiantes manifestaron dificultades en la comprensión de la noción de variable en los problemas que se les plantearon. Dificultades asociadas a los procesos de evolución del pensamiento algebraico en los estudiantes, que provocan que los conocimientos adquiridos, en una determinada etapa, se conviertan en modelos implícitos inadecuados para adquisición de nuevos conocimientos (Cajaraville, et al., 2012).
Según Godino y Font (2004) y Cajaraville et al., (2012) las primeras experiencias con el razonamiento algebraico están relacionadas con la aritmética generalizada y estas experiencias de los estudiantes con la aritmética son importantes para la comprensión progresiva del lenguaje algebraico, y el concepto matemático que hace posible esta generalización es el de variable. Así, el uso de las letras en matemáticas parece ser ineludible, la simbología literal es un recurso potente que facilita la resolución de problemas. Sin embargo, a las letras suele darse diferentes usos. Küchemann (1980) pone de manifiesto que la interpretación y comprensión del uso de las letras en contexto algebraico progresa mediante seis etapas (la letra: evaluada, no usada, objeto, incógnita, número generalizado, y variable). Autores como Enfedaque (1990), Azarquiel (1991), Ursini y Trigueros (1998), Usiskin (1999), Rojas, Rodríguez, Romero, Castillo y Mora (1999) y Kieran (2006), Cajaraville et al., (2012) han estudiado la categorización y definición del uso de las letras propuesta por Küchemann (1980):
• La letra evaluada: A la letra se le da un valor numérico en lugar de tratarla como un valor desconocido. Por ejemplo, Si e+f=8 entonces e+f+g=?.
• Letra no usada: Aquí la letra se ignora, o a lo más es reconocida (pero sin dársele un significado). Por ejemplo, Si multiplicado por 4 puede ser escrito por . Multiplica por 4n la expresión n+5.
• Letra como objeto: La letra es vista como un nombre para un objeto, o como el objeto propiamente dicho. Por ejemplo, Una manzana cuesta C$15 córdobas y una pera C$ 20 córdobas. Si “x” es el número de manzanas y “y” el número de peras. ¿Qué representa la expresión 15x+20y?.
• La letra como incógnita: Aquí la letra se piensa como un número particular pero desconocido y el estudiante se lanza a operar con letra vista de esta manera, a pesar de la falta de cerradura del resultado. Por ejemplo, ¿Cuánto es verdadera la siguiente expresión?: L+M+N=L+P+N. Subraya la respuesta correcta: siempre; nunca; a veces; cuando, …
• La letra como número generalizado: La letra se ve como representante de valores o capaz de tomar varios valores más que como un valor específico. Por ejemplo, ¿Qué puede decirse acerca de c si y c+d=10 y c es menor d?.
• Letra como variable: La letra como variable representa un rango de valores y el estudiante es capaz de describir el grado con el cual los cambios en un conjunto se determinan por los cambios en otro (lo cual significa establecer al menos una relación de segundo orden). Por ejemplo, Si a+b=3 ¿Qué pasa con a si b se incrementa en 2?.
• Letra usada como relación funcional: -f(x)= x · sen(x)- en donde la letra x varía en determinado conjunto de números y, para cada valor de x, f(x) está ligada a este valor mediante la relación expresada por x · sen(x) (Cajaraville et al., 2012, p. 25).
La importancia que tiene lograr la comprensión en la generalización que desempeña la letra como variable, es una tarea difícil para muchos estudiantes, lo que se observa a través de los numerosos errores (conceptuales, procedimentales y estructurales) que cometen los estudiantes, han sido plasmados en diferentes investigaciones y documentos curriculares de amplia difusión internacional, como por ejemplo, Küchemann (1980), Furinghetti y Paula (1994), Schoenfeld y Arcavi (1999), Usiskin (1999), NCTM (2000), Bardini, Radford y Sabena (2005), Trigueros y Ursini (2006) entre otros.
Las relaciones entre la comprensión con lo afectivo hacia las matemáticas
Sería un error el creer que la solución de un problema es un asunto puramente intelectual, la determinación y las emociones juegan un papel importante. Una determinación un tanto tibia, un vago deseo de hacer los menos posibles pueden bastar a un problema de rutina que se plantea en la clase; pero para resolver un problema científico serio, hace falta una fuerza de voluntad capaz de resistir años de trabajos y de amargos fracasos (Polya, 1965, p. 80).
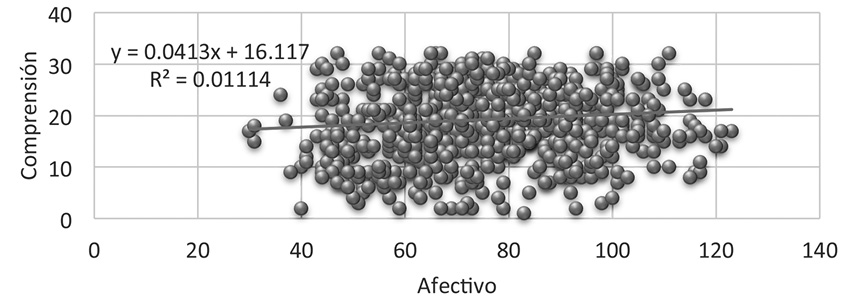
Figura no. 1. Relaciones entre la comprensión con lo afectivo hacia las matemáticas
Fuente: Elaboración propia.
En este contexto, en la figura no. 1, observamos que existe una relación lineal, es decir, una relación significativa, lo que se traduce: que al crecer el nivel de comprensión hacia los objetos matemáticos crecen los sentimientos y emociones hacia las matemáticas.
Teniendo en cuenta que en una situación ideal, y en una institución dada, diríamos que un sujeto “comprende” el significado del objeto –o que ha “captado el significado” de un concepto, por ejemplo- si fuese capaz de reconocer sus propiedades y representaciones características, relacionarlo con los restantes objetos matemáticos y usar este objeto en toda la variedad de situaciones problemáticas prototípicas dentro de la institución correspondiente (Godino y Batanero, 1994, p. 342).
Sin embargo, en este proceso de comprensión se manifiesta el papel afectivo hacia las matemáticas que se traduce en sentimientos y emociones, lo que conlleva a definirse como actitud hacia la matemática. Dicha actitud hacia las matemáticas se refiere a la valoración, el aprecio, la satisfacción, la curiosidad y el interés tanto por la disciplina como por su aprendizaje, acentuando más el componente afectivo que el cognitivo. La cuál la podemos medir en factores actitudinales como ansiedad, agrado, motivación, utilidad, confianza, que se definen en la figura no. 2.

Figura no. 2. Factores actitudinales hacia las matemáticas
Fuente: Elaboración propia.
Relaciones de la comprensión en los procesos de matemáticos
El proceso de matematización, consiste en traducir los problemas desde el mundo real al matemático, por lo que se sustenta en varios procesos entre ellos: pensar y razonar, argumentar y justificar, comunicar, modelar, representar y resolver problemas (Alsina, 2004; Tobón, 2007; Niss, 2002; Silbey, 2003; Castro et al. 2012). Estos procesos matemáticos descritos, formalizan la matematización en la resolución de problemas matemáticos. Según Pajares, Sanz y Rico (2004), su utilidad se concreta en establecer capacidades y habilidades específicas que ayudan a modular los objetivos, a establecer tareas escolares y caracterizar las propuestas de trabajo y las evaluaciones.
La comprensión posee una estrecha relación con los procesos de matematización, debido que los estudiantes deben matematizar o conceptualizar las situaciones, es decir, reconocer y extraer las matemáticas contenidas en una situación del mundo real. Por tale razones, los estudiantes tienen que trabajar en problemas que se le asocien tres aspectos:
• Reproducción, se trabaja con operaciones comunes, cálculos simples y problemas propios del entorno inmediato y la rutina cotidiana.
• Conexión, involucran ideas y procedimientos matemáticos para la solución de problemas que ya no pueden definirse como ordinarios pero que aún incluyen escenarios familiares; además involucran la elaboración de modelos para la solución de problemas.
• Reflexión, implican la solución de problemas complejos y el desarrollo de una aproximación matemática original.
No obstante, en la apropiación de la comprensión del conocimiento matemático en el contexto algebraico, se pueden exteriorizar: las actitudes hacia las matemáticas; dificultades de interpretación de las letras; dificultades debidas a la naturaleza del lenguaje algebraico en el contexto de las matemáticas; dificultades que tienen origen en la aritméticas, dificultades en el proceso de generalización y errores procedimentales.
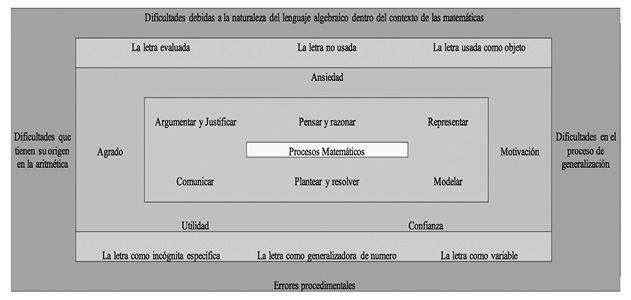
Figura no. 3. Relaciones entre la comprensión con los procesos matemáticos
Fuente: Elaboración propia
III. Conclusiones
Hemos presentado, de manera resumida, una serie de investigaciones con relación a los problemas asociados a la comprensión del álgebra. Cabe destacar que los problemas que se han detectado sugieren que deberían considerarse desde la enseñanza. Podríamos concluir que:
La noción de comprensión juega un papel importante en el aprendizaje de los conceptos-definiciones algebraicas, es decir, para que un estudiante obtenga un alto nivel de comprensión es necesario que pueda usar los procesos de matematización (pensar y razonar, argumentar y justificar, comunicar, modelar, plantear y resolver problemas, representar) en diferentes prácticas operativas y discursivas a las que este se enfrenta.
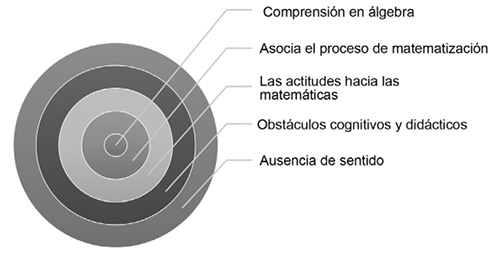
Figura no. 4. La comprensión como un procesos de matematización Fuente: Elaboración propia.
Sin embargo, durante este proceso de comprensión de las definiciones algebraicas, se manifiestan actitudes hacia las matemáticas que se tipifican en: ansiedad, agrado, motivación, utilidad y confianza hacia las matemáticas. Actitudes hacia las matemáticas que producen en el aprendizaje del álgebra obstáculos cognitivos y didácticos, así como una ausencia de sentido que se originan en los distintos estadios (semiótico, estructural, autónomo) que se dan en los sistemas de representación, todo ello, lo podemos diferencia en las etapas siguientes:
• Dificultades del álgebra que tienen su origen en la aritmética.
• Errores procedimentales: relativos al mal uso de la propiedad distributiva, relativo al uso de recíprocos, errores de cancelación.
• Dificultades debidas a la naturaleza del lenguaje algebraico dentro del contexto de las poblaciones en diversidad lingüística y étnica.
• Dificultades en el proceso de generalización
En este sentido, es necesario promover el reconocimiento de la diversidad en la clases de matemática a partir del Diseño para Todos y el Diseño con Todos para la enseñanza de las matemáticas en la Universidad, promoviendo situaciones encontradas en la vida diaria, incluidos los contextos profesionales, los cuales requieren un cierto agrado de comprensión de las matemáticas, razonamiento matemáticos y herramientas matemáticas antes todo de poder entenderlas y abordarlas en su totalidad.
IV. Lista de referencias
Alsina, A. (2004). Desarrollo de competencias matemáticas con recursos lúdicos-manipulativos. Madrid: Narcea.
Azarquiel, Grupo. (1991). Ideas y actividades para enseñar algebra. Madrid: Síntesis.
Batanero, C., y Díaz, C. (2006). Análisis del proceso de construcción de un cuestionario sobre probabilidad condicional. Revista de Educación Matemática. 8 (2), 197-223.
Bardini, C., Radford, L., & Sabena, C. (2005). Struggling with variables, parameters, and indeterminate objects or how to go insane in mathematics. In H. Chick, and J. Vicent, (Eds.). Proceedings of the 29th Conference of the International Group for the Psychology of Mathematics Education. Vol. II, 129-136. Australia. Melbourne: Design and Print Centre, University of Melbourne.
Bolea, P., Bosch, M. & Gascón, J. (2001). La transposición didáctica de organizaciones matemáticas en procesos de algebrización: el caso de la proporcionalidad. Recherches en Didactique des Mathématiques. 21(3), 247-304.
Brousseau, G. (1983). Les obstacles épistémologiques et les problémes en mathématiques. Recherches en Didactique des Mathématiques. 4(2), 165-198.
Cajaraville, J., Cachafeiro, L., Fernández, T., Ferro, & Salinas, M. (2012). Problemática Didáctica del estudio del álgebra en Educación Secundaria. Santiago de Compostela: Imprenta Universitaria.
Castro, C., Molina, E., Gutiérrez, M., Martínez, S., & Escorial, B. (2012). Resolución de problemas para el desarrollo de la competencia matemática en educación infantil. Números: Revista de didáctica de las matemáticas, Vol. 80, 53-70.
Chevallard, G., Bosch, M. & Gascón, J. (1997). Estudiar matemáticas. El eslabón perdido entre enseñanza y aprendizaje. Barcelona: ICE-Horsi.
Duval, R. (1993). Registres de représentation sémiotique et fonctionnement cognitive de la pensé. Annales de Didactique et de Sciencies Cognitives. 5, 37-65.
Enfedaque, J. (1990). De los números a las letras. Suma, 5, 23-34.
Furinghetti, F. & Paula, D. (1994). Parameters, unknowns and variables: a Little differencé? In J. Da Ponte, and J. Matos, (Eds.). Proceedings of the 18th International Conference of the Psychology of Mathematics Education. Vol. II, 368-375. Portugal: Universidad de Lisboa.
Godino, J. (2002). Competencia y comprensión matemática: ¿Qué son y cómo se consiguen? UNO, 29, 9-19.
Godino, J., & Batanero, C. (1994). Significado institucional y personal de los objetos matemáticos. Researches en Didactique des Mathématique, 14 (3) 325-355.
Godino, J. & Font, V. (2004). Razonamiento algebraico para maestros. En J. Godino, (Eds.). Matemática y su didáctica para Maestros. Proyecto Edumat-Maestros (771-826). (http://www.ugr.es/local/jgodino/edumat-maestros).
Godino, J., Batanero, C., & Font, V. (2007). The onto-semiotic approach to research in mathematics education. ZDM. The International Journal on Mathematics Education. Vol. 39 (1-2), 127-135.
Janvier, C. (1987). Traslation Processes in Mathematics Education. In C. Janvier, (Eds.). Problems of Representation in the Teaching and Learning of Mathematics (27-32). Hillsdale, NJ: Lawrence Erlbaum Associates.
Kaput, J. (1999). Teaching and Learning a New Algebra. In E. Fennema, and T. Romberg, (Eds.). Mathematics Classrooms that Promote Understanding (135-155). Mahwa. NJ: Laurence Erbaum Associates Inc. Publishers
Kieran, C. (1981). Concepts associated with the equality symbol. Educational Studies in Mathematics, 12, 317-326.
Kieran, C & Filloy, E. (1989). El aprendizaje del álgebra escolar desde una perspectiva psicológica. Enseñanza de las Ciencias. 7(3), 58-81.
Kieran, C. (1992). The Learning and Teaching of School Algebra. In D. Grouws, (Eds.). Handbook of Research on Mathematics Teaching and Learning (390-419). New York: Macmillan Publishing Company.
Kieran, C. (1997). Mathematical concepts at the secondary school level: the learning of algebra and function. In T. Nunes, and P. Bryant, (Eds.). Learning and teaching mathematics: An international perspective (133-157). East Sussex UK: Psychilogy Press.
Kieran, C. (2006). Research on the learning and teaching of algebra. In A. Gutiérrez, and P. Boera, (Eds.). Handbook on the Psychology of Mathematics Education. Past, Present and Future (11-49). UK: Sense Publishers.
Küchemann, D. (1980). Children understands of numerical variables. Mathematics in school. 7(4), 23-26.
Niss, M. (2002). Mathematical competencies and the learning of mathematics. The Danish KOM Project, Denmark, IMFUFA, Roskilde, University.
NCTM (2000). Principles and standards for school mathematics. National Council of Teacher of Mathematics. Electronica: http://standards.nctm.org.
OECD. (2004). Learning for Tomorrow’s World: First results from PISA 2003. Paris: OECD.
OECD. (2005). Informe PISA 2003. Aprender para el mundo de mañana. Madrid: Santillana.
Pajarez, R., Sanz, A., & Rico, L. (2004). Aproximación a un modelo de evaluación: el proyecto PISA 2000. Madrid: Ministerio de Educación, Cultura y Deporte.
Palarea M., & Socas, M. (1994). Algunos obstáculos cognitivos en el aprendizaje del lenguaje algebraico. SUMA, 16, 91-98
Pizón M., & Gallardo, A. (2000). Semántica versus sintaxis en la resolución de ecuaciones lineales. Educación Matemática. 12(2), 81-96.
Rojas, P., Rodríguez, J., Romero, J., Castillo, E., & Mora, L. (1999). La transición del aritmética al álgebra. Grupo Pretexto. Bogotá: Gaia-Universidad Distrital.
Socas, M. (1997). Dificultades y errores en el aprendizaje de las Matemáticas en la Escuela de Secundaria. En L. Rico et al (Eds.). La educación matemática en la enseñanza secundaria (125-154). Barcelona: ICE-Horsori.
Schoenfeld, A & Arcavi, A. (1999). On the meaning of variable. In B. Moses (Ed.). Algebraic Thinking Grade K-12 (pp. 150-156). Reston (Virginia): National Council of Teachers of Mathematics (NCTM).
Skemp, R. (1976). Relational understanding and instrumental understanding. Mathematics Teaching.
Silbey, R. (2003). Math out loud! Instructor. Vol.112, 7, 24-26.
TIMSS. (2003). Marcos teóricos y especificaciones de evaluación de TIMSS 2003. Madrid: Ministerio de Educación, Cultura y Deporte-INCE.
Tobón, S. (2007). Formación basada en competencias. Pensamiento complejo, diseño curricular y didáctica. Colombia: Ecoe Ediciones.
Trigueros M., & Ursini, S. (2006). ¿Mejora la comprensión del concepto variable cuandolos estudiantes cursan matemáticas avanzadas? Revista Matemática Educativa. 18(3), 5-38.
Ursini, S., & Trigueros, M. (1998). Dificultades de los estudiantes universitarios frente al concepto de variable. Investigaciones en Matemática Educativa II. Mexico: CINVESTAV-IPN
Usiskin, Z. (1999). Conception of School Algebra and uses of variables. In B. Moses (Ed.). Algebra Thinking Grade K-12 (7-13). Reston (Virginia): National Council of Teachers of Mathematics (NCTM).
Vicario, M. (2002). Un estudio sobre la noción de variable en estudiantes de nivel medio y superior. Tesis de Grado. México: FM-UA (No publicado).
1 Doctor en Educación, Gestor de proyectos de la Dirección de Cooperación Externa en la Universidad de las Regiones Autónomas de la Costa Caribe Nicaragüense, correo: william.flores@uraccan.edu.ni
2 Doctora en Psicología. Vicerrectora de Ordenación Académica, Innovación Docente y Calidad de la Universidad de Deusto, España, correo: elena.auzmendi@deusto.es
