RESOLUCIÓN DE PROBLEMAS MATEMÁTICOS: UN CUESTIONARIO PARA SU EVALUACIÓN Y COMPRENSIÓN
William Oswaldo Flores López 1
Elena Auzmendi Escribano 2
Resumen
Este artículo abordó el análisis de un instrumento de evaluación cuyo propósito fue explorar y caracterizar los procesos de resolución de problemas matemáticos. Se trata de un estudio cuantitativo y cualitativo, con una muestra de 80 estudiantes universitarios de la Universidad de las Regiones Autónomas de la Costa Caribe Nicaragüense, recinto Nueva Guinea. El análisis se desarrolló a partir del índice de dificultad, índice de discriminación, fiabilidad, validez de contenido, validez de constructo y análisis de las puntuaciones totales. Los resultados sostienen que la noción de comprensión es el hilo argumental del diseño, implementación y evaluación de los procesos de resolución de problemas matemáticos en el contexto algebraico, y se explica en términos epistémicos, ecológicos, afectivos, cognitivos, interaccional y mediacional; en cuanto instrumento de evaluación tiene como finalidad proporcionar información sobre los significados personales de un grupo de estudiantes sobre un objeto o un grupo de objetos matemáticos.
Palabras clave: comprensión, procesos matemáticos, contexto algebraico, idoneidad didáctica.
Summary
The following article discussed the analysis of an evaluation tool with the purpose to explore and characterize the processes of resolving mathematical problems or exercises. This is a quantitative and qualitative study, with a sample of 80 students from the University of the Autonomous Regions of the Caribbean Coast of Nicaragua, Nueva Guinea campus. The analysis was developed based on the difficulty index, discrimination index, reliability, validity of the content and construct, as well as the analysis of the total scores.
The results indicates that the comprehension notion is the storyline of the design, implementation and evaluation of the processes of resolving mathematical problems in algebraic context, and its explained in an epistemological, ecological, affective, cognitive, interactional and mediational terms. Meanwhile, in terms of evaluation tools it aims to provide information related to personal meanings of a group of students on an object or pertaining a group of mathematical objects.
Keywords: Comprehension, mathematical processes, algebraic context, educational suitability.
I. Introducción
La didáctica de las matemáticas estudia el significado que los estudiantes atribuyen a los objetos matemáticos (conceptos, propiedades); asimismo explica la construcción de estos significados como consecuencia de la instrucción. En Godino (2003) se propone que si aceptamos que un sujeto comprende o capta el significado de un objeto cuando es capaz de reconocer sus propiedades y representaciones, relacionarlos con otros objetos, y aplicarlo a una variedad de situaciones problemáticas prototípicas, estaremos relacionando la idea de significado con la de comprensión.
La importancia que tiene la noción de comprensión para la didáctica de las matemáticas está plasmada en diferentes investigaciones y documentos curriculares de amplia difusión internacional como en NCTM (2000), TIMSS (2003) y OECD (2004), señalan que los estudiantes deberían de comprender las matemáticas; sin embargo, la realidad del aula parece distanciarse de estos planteamientos. La práctica del aula parece decantarse hacia la práctica rutinaria de ejercicios algorítmicos, con clara predominancia del marco aritmético-algebraico, promoviendo casi en exclusiva la comprensión instrumental (Skemp, 1976). Esto se debe a que no hay cursos básicos que tengan como anterioridad del desarrollo científico, la lógica simbólica. Luego, los enfoques rutinarios de los docentes.
Consciente del escenario anterior, en este artículo nos centramos, en particular, en el estudio de las relaciones entre los procesos matemáticos y la práctica de resolución de problemas por parte de estudiantes universitarios. Todo ello, con la premisa de que un instrumento de evaluación tiene como finalidad proporcionar información sobre los significados personales de un grupo de estudiantes sobre un objeto o un grupo de objetos matemáticos dados (Godino, 2003; Godino, Batanero & Roa, 2005; Batanero & Díaz, 2006).
II. Revisión de literatura
En la OECD (2005) el conocimiento matemático es evaluado en función de tres dimensiones: el contenido al que se refieren los problemas matemáticos; los procesos que deben activarse para conectar los fenómenos observados con las matemáticas y resolver así problemas correspondientes; y, por último, las situaciones y los contextos utilizados como fuente de materiales de estímulo y en los que se plantean los problemas.
Concerniente al contenido, nos basamos en la ideas de Frege (1996) sobre sentido y referencia, el cual sostiene que los diferentes significados de un concepto matemático vienen dados por las estructuras conceptuales que se inserta, por los sistemas de símbolo que lo representan, y por los objetos y fenómenos de los que surge y que le dan sentido. Para Rico (2006) la terna de Frege Signo-Sentido-Referencia, para caracterizar el significado de un concepto matemático lo adecua para las matemáticas en contexto educativos. En esta reflexión sobre contenidos, que corresponde al estudio curricular, el significado de un concepto matemático educativo se establece mediante la terna Representación-Fenómeno-Definición.
También Rico (1997), dice que resulta difícil asumir que hay multiciplidad de significados para un mismo concepto matemático, ya que hay diversos sistemas de signos para su representación e, igualmente hay diversos objetos (fenómenos) que refieren y dan distintos sentidos a un mismo concepto. Por eso es factible entender que hay pluralidad de significados para un mismo concepto matemático. Determinar los significados más relevantes de cada concepto es uno de los retos de la enseñanza-aprendizaje de las matemáticas, es decir, una tarea de investigación del profesor de matemáticas para así trasmitir a los estudiantes los significados culturales y científicos de las matemáticas. “Entender diferentes significados de un mismo concepto proporciona su comprensión” (Rico, 2006, p. 285). En este contexto, las ideas fundamentales adoptada por OECD (2005), que satisfacen las condiciones de respetar el desarrollo histórico, cubrir el dominio y contribuir a la reflexión de las líneas principales del currículo escolar, son: cantidad, espacio y forma, cambios y relaciones, incertidumbre.
El conjunto de las cuatro áreas de contenidos cubre el abanico de las necesidades matemáticas de los estudiantes como base para su vida y para ampliar su horizonte de las matemáticas. Los conceptos pueden relacionarse con áreas como la aritmética, el álgebra o la geometría, y sus correspondientes sub-áreas, que reflejan las ramas definidas del pensamiento matemático y que facilitan el desarrollo de un programa de enseñanza estructurado. En general, estas categorías de contenidos aseguran que las tareas utilizadas para la evaluación tienen una distribución suficiente a lo largo del currículo, pero al mismo tiempo en un número no muy amplio que evite una división excesiva. Las cuatro áreas establecen los valores considerados para la variable contenido, que es una de las que identifican las tareas y determinan la evaluación (Rico, 2006).
La evaluación de las matemáticas exige que los estudiantes se enfrenten a problemas matemáticos basados en un contexto del mundo real, en que tienen que identificar las características de la situación del problema que podría ser susceptible de investigación matemática y activar los procesos matemáticos necesarios (OECD, 2004). Para hacerlo, deben llevar a cabo un proceso de matematización, el cual consiste en traducir los problemas desde el mundo real al matemático, por lo que se sustenta en varios procesos entre ellos: pensar y razonar, argumentar y justificar; comunicar; modelizar; representar; y resolver problemas (Alsina, 2004; Tobón, 2007; Niss, 2002; Silbey, 2003; Castro et al. 2012). Estos procesos matemáticos descritos, formalizan la matematización en la resolución de problemas matemáticos. Según Pajares, Sanz y Rico (2004) su utilidad se concreta en establecer capacidades y habilidades específicas que ayudan a modular los objetivos, a establecer tareas escolares y caracterizar las propuestas de trabajo y las evaluaciones.
Referente a la situación o problema, existen cuatro tipos de situaciones: personales, educativas u ocupacionales, públicas y científicas. Es decir, la variable situación-problema toma cuatro valores, que permiten establecer la localización de un problema en términos de los fenómenos de los que surge la situación problemática considerada (OECD, 2004). La aproximación fenomenológica y los contextos y situaciones donde se plantean los problemas constituyen los ejes centrales que dotan de sentido al conocimiento matemático (Rico, 2006). Está prioridad se basa en la consideración funcional de las matemáticas educativas, que destaca la importancia de conceptos procedimientos matemáticos como herramientas para dar solución a problemas.
III. Materiales y métodos
La naturaleza de la temática de nuestra investigación, reclama la integración sistemática de los métodos cualitativos y cuantitativos en un solo estudio con el fin de obtener una fotografía más completa del fenómeno (Hernández, Fernández, & Baptista, 2010). La integración del método cualitativo permitirá describir e interpretar la realidad educativa con el fin de llegar a la comprensión o a la transformación de dicha realidad, a partir del significado atribuido por las personas que la integran (Bisquerra, 2009). Y el método cuantitativo nos ayudará al tratamiento de los datos a través de la categorización y descripción de las propiedades, características y los perfiles de las personas, grupos, comunidades, procesos y objetos o cualquier otro fenómeno que se someta a un análisis (Hernández, Fernández, & Baptista, 2010).
El estudio se llevó a cabo con una muestra de 80 estudiantes universitarios de los Grados en Informática Administrativa e Ingeniería Agroforestal de la Universidad de las Regiones Autónomas de la Costa Caribe Nicaragüense, pertenecientes a comunidades de la Región Autónoma del Caribe Norte de Nicaragua. La selección para el muestreo de las especialidades se realizó mediante un muestreo aleatorio estratificado, tomando como estrato de selección especialidad (Informática Administrativa e Ingeniería Agroforestal) y el haber cursado la asignatura de matemática para la vida. La edad media entre los participantes fue de 17 años, con un rango de edad comprendido entre los 16 y los 19 años. La distribución por especialidad se resume en el cuadro No. 01. El 61% de los participantes fueron hombres y el 39% restante fueron mujeres.
Cuadro No. 01: Distribución por especialidad
|
Hombres |
Mujeres |
Total |
% |
||
|
Válidos |
Informática Administrativa |
18 |
21 |
39 |
49 |
|
Ingeniería Agroforestal |
31 |
10 |
41 |
51 |
|
|
Total |
49 |
31 |
80 |
100% |
|
|
% |
61 |
39 |
Fuente: Elaboración propia.
El instrumento de evaluación utilizado para observar los procesos de resolución de problemas matemáticos de la muestra de estudiantes de Informática Administrativa e Ingeniería Agroforestal, ha consistido en un cuestionario que mide contenidos relacionados al álgebra. Se trata de un cuestionario compuesto por 32 ítems en que se consideran los contenidos que se reflejan en el cuadro No. 02.
Cuadro No. 02: Contenido evaluado en el instrumento
|
Contenido Evaluado |
Ítems |
|
Propiedades de la adición y la multiplicación en R. |
1, 2, 4, 5, 8, 26. |
|
Propiedades de orden de los números reales. |
14, 22, 23, 24. |
|
Proposiciones y funciones proposicionales |
3, 6, 7, 10, 13, 15, 18, 19, 20, 25, 27, 32. |
|
Ecuaciones de primer grado con una incógnita |
9, 11, 16, 17, 29. |
|
Resolución algebraica de problemas verbales |
12, 21,28, 30, 31. |
Fuente: Elaboración propia.
El análisis del cuestionario se efectuó usando la teoría clásica de los test entre los tipos de análisis se destaca: el análisis de dificultad, análisis de discriminación, análisis de fiabilidad, validez de contenido, validez de constructo y análisis de las puntuaciones totales (Muñiz, 1994; Barbero, 2003; Gill, 2011). Por tanto, se utilizaron herramientas tecnológicas como SPSS, Statgraphics y Atlas. Ti para realizar dichos análisis. También se realizó una reflexión desde la perspectiva de la idoneidad didáctica (Godino, 2011).
IV. Resultados
Análisis del índice de dificultad
El índice de dificultad valora la dificultad que entraña la resolución de ítem para la población a la que va dirigida el cuestionario (Muñiz, 1994). Este índice, permite ordenar los ítems en función de su dificultad y puede ayudar a la selección de ítems en función de los objetivos y facilitan la discriminación. Puesto que el índice de dificultad es una proporción (la proporción de estudiantes que superan el ítem) calculamos adicionalmente los intervalos de confianza de dicha proporción con la fórmula habitual, véase el cuadro No. 03.
Cuadro No. 03: Proporciones de acierto con intervalos de confianza del 95%
|
k |
p |
L(-) |
L(+) |
k |
p |
L(-) |
L(+) |
k |
p |
L(-) |
L(+) |
k |
p |
L(-) |
L(+) |
|
1 |
0,68 |
0,57 |
0,78 |
9 |
0,63 |
0,52 |
0,73 |
17 |
0,60 |
0,49 |
0,71 |
25 |
0,30 |
0,20 |
0,40 |
|
2 |
0,73 |
0,63 |
0,83 |
10 |
0,40 |
0,29 |
0,50 |
18 |
0,43 |
0,31 |
0,54 |
26 |
0,89 |
0,82 |
0,95 |
|
3 |
0,88 |
0,80 |
0,95 |
11 |
0,68 |
0,57 |
0,78 |
19 |
0,40 |
0,29 |
0,51 |
27 |
0,61 |
0,50 |
0,72 |
|
4 |
0,60 |
0,49 |
0,70 |
12 |
0,40 |
0,29 |
0,51 |
20 |
0,60 |
0,49 |
0,71 |
28 |
0,50 |
0,39 |
0,61 |
|
5 |
0,38 |
0,26 |
0,48 |
13 |
0,68 |
0,57 |
0,78 |
21 |
0,50 |
0,39 |
0,61 |
29 |
0,63 |
0,52 |
0,73 |
|
6 |
0,63 |
0,52 |
0,73 |
14 |
0,73 |
0,63 |
0,83 |
22 |
0,63 |
0,52 |
0,73 |
30 |
0,40 |
0,29 |
0,51 |
|
7 |
0,26 |
0,16 |
0,36 |
15 |
0,33 |
0,22 |
0,43 |
23 |
0,40 |
0,29 |
0,51 |
31 |
0,85 |
0,77 |
0,93 |
|
8 |
0,33 |
0,22 |
0,42 |
16 |
0,30 |
0,20 |
0,40 |
24 |
0,60 |
0,49 |
0,71 |
32 |
0,86 |
0,79 |
0,94 |
Fuente: Flores & Auzmendi.
Según Gil (2011), los valores del índice de dificultad de un ítem se suelen clasificar en cinco categorías: Muy fáciles (por encima de 0,75), Fáciles (comprendido entre 0,55 y 0,75), Normales (comprendido entre 0,45 y 0,54), Difíciles (comprendido entre 0,25 y 0,44) y Muy difíciles (por debajo de 0,25). Los índices de dificultad media son los que discriminan mejor (Batanero & Díaz, 2006). En este contexto, se presenta en la figura No. 1, donde se refleja la distribución de las categorías después de haber estimado las proporciones de acierto.

Figura No. 01: Categoría de dificultad de ítem.
Fuente: Elaboración propia.
Los resultados ponen de manifiesto que el 13% del total de los ítems son muy fáciles, un 44% del total demuestra una tendencia de fáciles, mientras que un 6% está razonablemente normal. Sin embargo, existe un 38% del total de los ítems difíciles para los estudiantes participantes en el estudio. En resumen, se puede decir que en conjunto la dificultad es medio-alta, puesto que los índices van de una dificultad difícil hasta una dificultad muy fácil, no hay ítem con dificultad muy difícil (índices inferiores al 25%). En la figura No. 2 se presenta la distribución de estos índices, que abarcan todo el posible rango de variación, con algo más de concentración en el intervalo 20-25 con una normalidad aproximada.

Figura No. 2: Distribución del índice de dificultad.
Fuente: Elaboración propia.
Y la prueba de Kolmogorov-Smirnov confirman la existencia de una normalidad aproximada (véase cuadro No. 04).
Cuadro No. 04: Prueba de Kolmogorov-Smirnov para una muestra (32 ítems)
|
Parámetros normales (a, b) |
Media |
17,77 |
|
Desviación estándar |
6,70 |
|
|
Máximas diferencias extremas |
Absoluta |
0,118 |
|
Positivo |
0,055 |
|
|
Negativo |
-0,118 |
|
|
Estadístico de prueba |
0,118 |
|
|
Sig. asintótica (bilateral) |
0,008 |
|
Fuente: Elaboración propia.
Análisis del índice de discriminación
El índice de discriminación se calculó mediante la correlación corregida entre el ítem y la puntuación total del cuestionario, calculada a partir de las correlación de Pearson. Todos los ítems tienen una correlación positiva (véase cuadro No. 05, rix). En la mayoría de los ítems la correlación no llega a ser estadísticamente significativa e incluso inexistente (rix >0,05). Esto puede ser debido, a que los estudiantes aparecen con buenos resultados en el total del cuestionario.
Cuadro No. 05: Índice de homogeneidad
|
K |
IH |
K |
IH |
||||||
|
1 |
0,457 |
6,702 |
0,471 |
0,399 |
17 |
0,647 |
6,702 |
0,493 |
0,601 |
|
2 |
0,450 |
6,702 |
0,449 |
0,394 |
18 |
0,321 |
6,702 |
0,497 |
0,252 |
|
3 |
0,163 |
6,702 |
0,333 |
0,114 |
19 |
0,449 |
6,702 |
0,493 |
0,387 |
|
4 |
0,647 |
6,702 |
0,493 |
0,601 |
20 |
0,647 |
6,702 |
0,493 |
0,601 |
|
5 |
0,499 |
6,702 |
0,487 |
0,441 |
21 |
0,522 |
6,702 |
0,503 |
0,464 |
|
6 |
0,614 |
6,702 |
0,487 |
0,566 |
22 |
0,614 |
6,702 |
0,487 |
0,566 |
|
7 |
0,528 |
6,702 |
0,443 |
0,478 |
23 |
0,303 |
6,702 |
0,493 |
0,234 |
|
8 |
0,504 |
6,702 |
0,471 |
0,449 |
24 |
0,647 |
6,702 |
0,493 |
0,601 |
|
9 |
0,300 |
6,702 |
0,487 |
0,232 |
25 |
0,374 |
6,702 |
0,461 |
0,313 |
|
10 |
0,503 |
6,702 |
0,493 |
0,445 |
26 |
0,338 |
6,702 |
0,318 |
0,295 |
|
11 |
0,530 |
6,702 |
0,471 |
0,477 |
27 |
0,311 |
6,702 |
0,490 |
0,243 |
|
12 |
0,303 |
6,702 |
0,493 |
0,234 |
28 |
0,522 |
6,702 |
0,503 |
0,464 |
|
13 |
0,457 |
6,702 |
0,471 |
0,399 |
29 |
0,614 |
6,702 |
0,487 |
0,566 |
|
14 |
0,450 |
6,702 |
0,449 |
0,394 |
30 |
0,449 |
6,702 |
0,493 |
0,387 |
|
15 |
0,504 |
6,702 |
0,471 |
0,449 |
31 |
0,212 |
6,702 |
0,359 |
0,160 |
|
16 |
0,260 |
6,702 |
0,461 |
0,194 |
32 |
0,439 |
6,702 |
0,347 |
0,396 |
Fuente: Elaboración propia.
También se calculó el índice de homogeneidad (IH) a partir de la correlación ítems-test, desviación estándar del test y la desviación estándar de cada uno de los ítems (véase el cuadro No. 6). Consecuentemente se clasificó el índice de la homogeneidad en los siguientes valores: el 47% de los ítems discriminan muy bien (igual o mayor de 0,4); un 25% discriminan bien (comprendido entre 0,3 y 0,39); un 19% discrimina poco (comprendido entre 0,2 y 0,29); y el 9% del total de los ítems se deben mejorar (comprendido entre 0,10 y 0,19). En general, los ítems poseen una buena discriminación en el instrumento. Véase la figura No. 3.

Figura No. 3: Índice de discriminación.
Fuente: Elaboración propia.
Análisis de fiabilidad
Se entiende por fiabilidad de un test, un cuestionario o instrumento de medida a la estabilidad de las puntuaciones observadas, en el sentido de proporcionar un valor numérico que indica el grado de confianza que se puede tener en dichas puntuaciones como estimadores de las puntuaciones verdaderas de los sujetos. En Batanero y Díaz (2003) se expresa que este coeficiente de fiabilidad es valor teórico que debe ser estimado por algún procedimiento empírico, a través de las respuestas de un grupo de sujetos a un conjunto de ítems. Entre los diversos procedimientos para el cálculo del estimador del coeficiente de fiabilidad se utilizó primeramente el coeficiente de Kuder-Richardson para ítems dicotómicos. El cual refleja el grado de variación de los ítems que constituye el test.
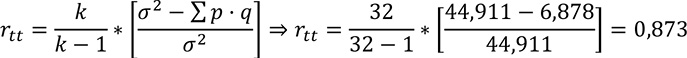
Cuando se sospecha que el cuestionario es multidimensional se puede calcular las siguientes razones, basados en los resultados del análisis factorial (Barbero, 2003; Batanero & Díaz 2006):
El coeficiente Theta que tiene en cuenta los pesos de los ítems en el primer factor (Carmines & Zeller, 1979). Se trata del coeficiente alfa cuando las varianzas verdaderas (suma de las covarianzas) y el total se calculan a partir de las puntuaciones factoriales derivadas del primer factor, antes de las rotaciones (Morales, 1988). En el caso del cuestionario de procesos de resolución de problemas fue bastante alto, debido a que el primer factor explica porcentajes de la varianza. Viene dado por la siguiente expresión, donde λ1 es el primer autovalor en el análisis factorial.

El coeficiente Omega, que en el cuestionario de procesos de resolución de problemas matemáticos cumplió con la relación: α < θ <Ω (Heise & Bohrnstedt, 1970). En la expresión que sigue, hj son las comunalidades de las variable (correlaciones múltiple de cada una con las demás) y rjh las correlaciones entre pares de variables.
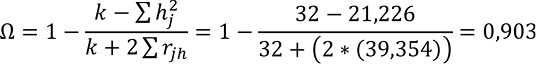
Análisis de la validez de contenido
La validez de contenido consistió en que el instrumento recogiera una muestra representativa de los contenidos evaluados (propiedades de adición y multiplicación, propiedades de orden, proposiciones y funciones proposicionales, ecuaciones de primer grado con una incógnita, resolución algebraica de problemas verbales) y su relación con los procesos matemáticos (pensar y razonar, argumentar, comunicar, modelar, representar, plantear y resolver problemas) que se desearon estudiar, está asociación se puede observar en la figura No. 4.
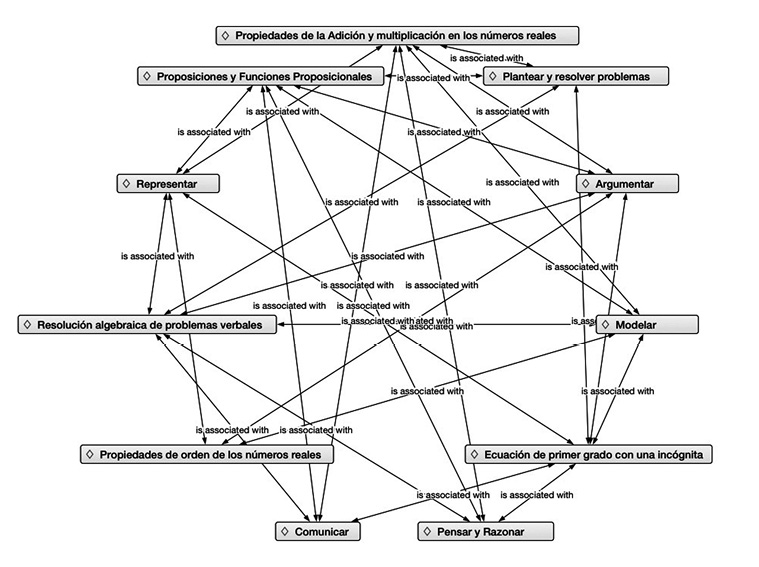
Figura No. 4: Relación entre el contenido evaluado y los procesos matemáticos.
Fuente: Elaboración propia.
Por consiguiente, se efectuó una planificación cuidadosa de los ítems que se incluyeron en el estudio y así mismo se planteó cómo éstos pueden contribuir a la medida del constructo subyacente. Para salvar la dificultad de determinar qué es un muestreo adecuado de ítems en el dominio particular, se describe la vinculación de los contextos donde se desarrolla el álgebra con los procesos matemáticos que se evaluó en cada ítem, a continuación:
1. El álgebra en un contexto de la aritmética generalizada
• Realizar cálculos sencillos que implican relaciones entre dos variables desconocidas.
• Utilizar una representación bidimensional dada para contar o calcular elementos de un objeto.
• Aplicar cálculos sencillos para resolver problemas en una conversión de registro en un contexto geométrico.
• Interpretar y aplicar fórmulas verbales así como manejar y utilizar fórmulas lineales que representen relaciones del mundo real.
• Aplicar algoritmos rutinarios para resolver problemas en contexto geométricos.
• Aplicar algoritmos rutinarios para relacionar diferentes representaciones de objetos.
2. El álgebra en un contexto de estudios de procedimientos para resolver problemas
• Determinar la cantidad desconocida que aparece en el problema realizando operaciones aritméticas y algebraicas.
• Sustituir la variable por el valor o los valores que hacen de la ecuación un enunciado verdadero, en un contexto de la propiedad conmutativa.
• Sustituir la variable por el valor o los valores que hacen de la ecuación un enunciado verdadero, en un contexto aditivo y multiplicativo.
• Interpretar la variable simbólica como la representación de una entidad general, indeterminada, que puede asumir cualquier valor.
• Interpretar las variables simbólicas que aparecen en una ecuación como la representación de valores específicos.
• Simbolizar las cantidades desconocidas identificadas en una situación específica y utilizarlas para plantear ecuaciones.
• Reconocer e identificar en una situación problemática la presencia de algo desconocido que puede ser determinado considerando las restricciones del problema.
3. El álgebra en un contexto de estudio de relaciones entre cantidades
• Utilizar términos y definiciones, técnicas básicas y aplicar conceptos geométricos básicos.
• Sustituir correctamente los números para explicar las relaciones entre dos variables desconocidas.
• Interpretar las relaciones entre dos variables a través de la sustitución de un número conocido.
• Analizar un modelo matemático dado que implique una fórmula compleja, es decir, deducir reglas y métodos generales en secuencias de familias de problemas.
• Utilizar representaciones múltiples para resolver un problema práctico, es decir, interpretar y comprender significados.
• Interpretar representaciones complejas para resolver un problema práctico.
• Realizar cálculos sencillos que implican relaciones entre una variable conocida. Situación algebraica en contexto de la propiedad conmutativa.
• Manipular (simplificar, desarrollar) la variable simbólica en situaciones algebraicas en contexto aditivo y multiplicativo.
• Usar comprensivamente el álgebra para resolver problemas; capacidad de manejar expresiones algebraicas para traducir una situación del mundo real.
• Interpretar información matemática compleja en el contexto de una situación real desconocida.
• Aplicar la comprensión geométrica para trabajar con patrones complejos y generalizados.
4. El álgebra en un contexto de estudio de estructuras
• Identificar los cálculos simples necesarios para resolver un problema sencillo en contexto multiplicativo.
• Sustituir correctamente los números para aplicar un algoritmo numérico o fórmula algebraica sencilla.
• Realizar cálculos sencillos que se incluyan en las operaciones aditivas.
• Realizar cálculos sencillos que implican operaciones aditivas: operaciones de las variables en campo numérico.
• Llevar a cabo cálculos explícitamente descritos que comprenden procesos secuenciales.
• Utilizar los datos relevantes de la descripción de una situación compleja y realizar los cálculos correspondientes.
• Reflexionar sobre la relación entre una fórmula algebraica y los datos subyacentes.
Análisis de validez de constructo
Se aplicó la técnica multivariante del análisis factorial, para reducir, estandarizar y validar la información recogida en el cuestionario aplicado a los estudiantes universitarios. El análisis factorial se ha llevado a cabo según el método de componentes principales (PrC) con fines confirmatorios. Por otro lado, la determinación de la cantidad de factores se ha realizado según el criterio de raíz latente de Kaiser-Meyer-Olkin. Y posteriormente, se ha aplicado la rotación Varimax (máxima varianza) con normalización de Kaiser. A continuación se presentan los resultados.
Cuadro No. 06: Resumen estadístico del análisis factorial
|
Medida de Adecuación Muestral |
Kaiser-Meyer-Olkin |
0,531 |
|
Prueba de Esfericidad de Bartlett |
Chi-cuadrado aproximado |
975,123 |
|
Gl |
496 |
|
|
Sig. |
0,000 |
|
|
Varianza Explicada Total |
% |
62% |
|
Fiabilidad |
Kuder-Richardson |
0,873 |
|
Heise-Bohrnstedt, |
0,891 |
|
|
Carmines-Zeller |
0,903 |
|
|
Cantidad de Niveles |
6 |
|
|
Cantidad de ítems |
32 |
|
Fuente: Elaboración Propia.
En el cuadro No. 07, se resumen las estadísticas de la solución factorial definitiva, después de la rotación, se puede observar que la solución definitiva del análisis factorial contiene 6 niveles con 32 de los ítems originalmente utilizados, los cuales explican un porcentaje de la varianza muy aceptable de un 66,326%. La prueba de esfericidad de Bartlett nos confirma sin duda la existencia de factores subyacentes en la matriz de datos, debido al alto nivel de significación obtenido (Cuadro No. 06).
Cuadro No. 7: Resumen Factorial
|
Niveles |
Total |
% Total de la Varianza |
% Acumulado |
|
|
Nivel 1 |
8 |
7,299 |
22,808 |
22,808 |
|
Nivel 2 |
7 |
4,215 |
13,173 |
35,982 |
|
Nivel 3 |
6 |
3,337 |
10,429 |
46,411 |
|
Nivel 4 |
3 |
2,574 |
8,043 |
54,454 |
|
Nivel 5 |
3 |
2,008 |
6,274 |
60,728 |
|
Nivel 6 |
5 |
1,791 |
5,598 |
66,326 |
Fuente: Elaboración propia.
Como puede observarse en el cuadro No. 8, los tres primeros niveles son los que más varianza explican, sólo entre ellos se alcanza el 46,411% de la varianza explicada; sin embargo, los otros tres factores también explican un porcentaje nada despreciable de un 19,915% entre ambos. La estructurada factorial hallada, coincide absolutamente con la planteada teóricamente, emergida en seis niveles coincidentes con los niveles de resolución de problemas matemáticos en el modelo de competencia matemática. Los niveles de complejidad de resolución de problemas se asociación con los procesos matemáticos cómo: razonar y pensar, argumentar, comunicar, modelizar y representar, véase esta asociación en la figura No. 5.
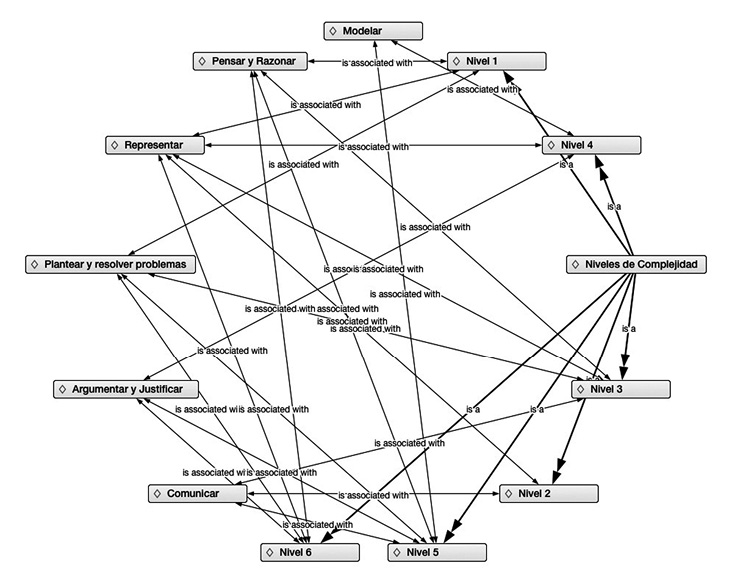
Figura No. 5: Procesos matemáticos en los niveles de complejidad de la resolución de problemas.
Fuente: Elaboración propia.
Los descriptores de los niveles establecidos se basan en la configuración del proceso de resolución de problemas en un contexto algebraico compuesto por un ciclo de seis subprocesos: Nivel 1 (definido en el primer factor), Nivel 2 (constituye el segundo factor), Nivel 3 (que está definido por el tercer factor), Nivel 4 (cuyos ítems satura el cuarto factor), Nivel 5 (definido en el quinto factor) y finalmente el Nivel 6 (que constituye el sexto factor).
Cuadro No. 08: Descripción de los factores
|
k |
N1 |
N2 |
N3 |
N4 |
N5 |
N6 |
|
I7 |
0,415 |
0,074 |
0,045 |
0,028 |
-0,007 |
-0,041 |
|
I8 |
0,437 |
0,005 |
0,087 |
0,050 |
-0,057 |
0,032 |
|
I5 |
0,530 |
0,024 |
-0,001 |
0,006 |
0,173 |
0,066 |
|
I6 |
0,937 |
0,008 |
0,071 |
0,057 |
0,060 |
0,049 |
|
I4 |
0,965 |
0,069 |
0,091 |
0,001 |
0,386 |
0,169 |
|
I1 |
0,933 |
0,105 |
0,097 |
0,111 |
-0,044 |
0,119 |
|
I2 |
0,930 |
0,028 |
0,333 |
0,236 |
-0,326 |
0,311 |
|
I3 |
0,409 |
0,149 |
0,195 |
0,371 |
-0,536 |
0,088 |
|
I15 |
0,149 |
0,437 |
0,195 |
0,371 |
-0,536 |
0,088 |
|
I14 |
0,005 |
0,930 |
0,087 |
0,050 |
-0,057 |
0,032 |
|
I12 |
0,085 |
0,776 |
-0,046 |
0,107 |
0,070 |
0,112 |
|
I13 |
0,074 |
0,933 |
0,045 |
0,028 |
-0,007 |
-0,041 |
|
I11 |
0,105 |
0,555 |
0,261 |
-0,052 |
0,203 |
0,077 |
|
I10 |
0,085 |
0,570 |
0,059 |
0,168 |
0,165 |
0,353 |
|
I9 |
0,134 |
0,318 |
0,025 |
0,235 |
-0,001 |
0,067 |
|
I20 |
0,071 |
0,008 |
0,965 |
0,057 |
0,060 |
0,049 |
|
I18 |
-0,039 |
-0,023 |
0,671 |
0,062 |
0,207 |
0,051 |
|
I21 |
0,114 |
0,186 |
0,830 |
0,126 |
0,194 |
0,185 |
|
I19 |
0,063 |
0,019 |
0,877 |
0,089 |
-0,101 |
0,125 |
|
I17 |
0,071 |
0,008 |
0,965 |
0,057 |
0,060 |
0,049 |
|
I16 |
0,208 |
-0,163 |
0,275 |
0,113 |
0,212 |
0,041 |
|
I24 |
0,057 |
0,008 |
0,071 |
0,965 |
0,060 |
0,049 |
|
I22 |
0,173 |
0,105 |
0,111 |
0,937 |
-0,044 |
0,119 |
|
I23 |
0,085 |
0,070 |
-0,046 |
0,776 |
0,107 |
0,112 |
|
I26 |
-0,017 |
0,192 |
0,432 |
0,169 |
0,435 |
-0,432 |
|
I25 |
0,042 |
0,302 |
0,227 |
-0,080 |
0,444 |
0,123 |
|
I27 |
0,143 |
-0,380 |
-0,039 |
-0,337 |
0,221 |
-0,113 |
|
I29 |
0,173 |
0,105 |
0,119 |
0,111 |
-0,044 |
0,937 |
|
I30 |
0,063 |
0,019 |
0,089 |
0,125 |
-0,101 |
0,877 |
|
I28 |
0,114 |
0,186 |
0,185 |
0,126 |
0,194 |
0,830 |
|
I31 |
-0,055 |
0,017 |
0,081 |
-0,091 |
0,237 |
0,311 |
|
I32 |
0,069 |
0,278 |
-0,380 |
0,476 |
0,190 |
0,374 |
Fuente: Elaboración propia.
• El primer factor, que explica el 22,808% de la varianza, comprende 8 ítems. En este factor se incluyen ítems en los que está presente toda la información pertinente y las preguntas están claramente definidas, es decir instrucciones directas en situaciones explicitas.
• El segundo, que describe el 13,173% de la varianza, compuesto por 7 ítems. Los ítems en este factor atributan a crear y expresar argumentos matemáticos a partir de algoritmos, fórmulas, procedimientos o convenciones elementales.
• El tercer factor, que significa el 10,429% de la varianza, comprende 6 ítems, este factor contienen ítems con representaciones basadas en diferentes fuentes de información y razonar directamente a partir de ellas.
• El cuarto factor, que representa el 8,043% de la varianza, está constituido por 3 ítems, estos enunciados hacen referencia a interpretar y trabajar con modelos explícitos en situaciones complejas y concretas que pueden conllevar condicionantes o exigir la formulación de supuesto.
• El quinto factor, que simboliza el 6,274% de la varianza, está formado por 3 ítems. En este factor los ítems incluyen situaciones reales o estructuras matemáticas que abordan problemas complejos relativos a estos modelos, es decir, representaciones adecuadas, relacionadas y caracterizadas en situaciones complejas.
• El sexto factor, que figura el 5,598% de la varianza, está representado por 5 ítems. Este factor contiene ítems con proposiciones y expresiones con símbolos y fórmulas utilizadas para realizar cálculos asociados a modelos de situaciones de problemas complejos.
Análisis de la puntuación total
Con el fin de determinar el efecto sobre la puntuación total en la prueba de los factores especialidad y género en que fue aplicada, se ha realizado un análisis de la varianza multifactorial para determinar qué factores tienen un efecto estadísticamente significativo sobre la puntuación total (variable dependiente, puntuación total). El cuadro No. 09 muestra la media de la puntuación total para cada uno de los niveles de los factores. También muestra los errores estándar de cada media, los cuales son una medida de la variabilidad en su muestreo. Las dos columnas de la derecha muestran intervalos de confianza del 95% para cada una de las medias:
Cuadro No. 09: Medias por mínimos cuadrado para la puntuación total
|
Error |
Límite |
Límite |
|||
|
Nivel |
Casos |
Media |
Est. |
Inferior |
Superior |
|
Media Global |
80 |
17,486 |
|
|
|
|
Especialidad |
|||||
|
Informática Administrativa |
39 |
18,777 |
1,057 |
16,671 |
20,882 |
|
Ingeniería Agroforestal |
41 |
16,196 |
1,107 |
13,991 |
18,400 |
|
Género |
|||||
|
Mujeres |
31 |
16,058 |
1,215 |
13,638 |
18,479 |
|
Hombres |
49 |
18,914 |
0,964 |
16,994 |
20,833 |
Fuente: Elaboración propia.
A partir del modelo de Dunn y Clarck (1987) para el análisis de varianza multifactorial de efectos fijos, hemos obtenido los componentes de la varianza (Cuadro No. 10). De está cuadro obtenemos los cuadrados medios entre sujetos para cada unos de los factores y residual, así como sus grados de libertad. No se ha evaluado la significación de las interacciones entre los factores. La prueba-F en el cuadro ANOVA permiten identificar los factores significativos.
Cuadro No. 10: Análisis de varianza para la puntuación total
|
Fuente |
Suma de Cuadrados |
Gl |
Cuadrado Medio |
Razón-F |
Valor-P |
|
Efectos Principales |
|||||
|
Especialidad |
120,985 |
1 |
120,985 |
2,78 |
0,0993 |
|
Género |
140,69 |
1 |
140,69 |
3,24 |
0,0759 |
|
Residuos |
3346,76 |
77 |
43,4644 |
||
|
Total (corregido) |
3547,95 |
79 |
Fuente: Elaboración propia.
En el cuadro No. 10 (ANOVA) se descompone la variabilidad de la puntuación total en contribuciones debidas a los factores considerados. Los valores-P indican la probabilidad de obtener un valor F tan extremo o más que el observado para cada uno de los factores. En nuestro caso no encontramos diferencias estadísticamente significativas entre los factores. Puesto que ningún valor-P es menor que 0,05, ninguno de los factores tiene efecto estadísticamente significativo sobre la puntuación total con un 95% de nivel de confianza. Por tanto se acepta la hipótesis de igualdad de puntuación media entre los factores. La prueba T de muestras independientes ratifica los resultados de la prueba de ANOVA, y esto se debe a que el valor de significancia de la prueba de Levene de calidad de varianza es mayor que 0,05 y así como la significancia de la prueba T para igualdad de medias con intervalo de confianza del 95%, véase el cuadro No. 11. En definitiva, se acepta que tanto hombres y mujeres que provienen de las especialidades en Informática Administrativa e Ingeniería Agroforestal parecen tener el mismo dominio de los procesos matemáticos para resolver situaciones-problemas en un contexto algebraico.
Cuadro No. 11: Prueba T para muestra independientes en la puntuación total
|
Prueba de Levene de calidad de varianzas |
Prueba T para la igualdad de medias |
|||||||||
|
F |
Sig. |
t |
gl |
Sig. |
Diferencia de medias |
Diferencia de error estándar |
95% de intervalo de confianza de la diferencia |
|||
|
Inferior |
Superior |
|||||||||
|
Especialidad |
Varianzas iguales |
1,399 |
0,240 |
1,163 |
78 |
0,248 |
1,740 |
1,496 |
-1,238 |
4,717 |
|
Varianzas desiguales |
1,167 |
77 |
0,247 |
1,740 |
1,491 |
-1,229 |
4,709 |
|||
|
Género |
Varianzas iguales |
0,059 |
0,809 |
-1,343 |
78 |
0,183 |
-2,055 |
1,530 |
-5,102 |
0,991 |
|
Varianzas desiguales |
-1,333 |
62 |
0,187 |
-2,055 |
1,542 |
-5,137 |
1,027 |
|||
Fuente: Elaboración propia.
V. Conclusiones
Las conclusiones que se presentan en este artículo se hacen a partir de la noción de idoneidad didáctica. La idoneidad didáctica de un proceso de evaluación, se define como la articulación coherente y sistémica de los criterios de idoneidad siguiente:
• La idoneidad cognitiva de un instrumento es el grado de dificultad que representan los ítems de dicho instrumento, es decir, el grado de representatividad de los significados evaluados respecto a los significados personales. En nuestro estudio los resultados ponen de manifiesto que el grado de dificultad del instrumento es medio-alta, puesto que los índices van de una dificultad difícil hasta una dificultad muy fácil, no hay ítem con dificultad muy difícil (índices inferiores al 25%). Y la prueba de normalidad confirma dicha distribución del grado de dificultad.
• La idoneidad evaluadora de un instrumento es el índice de discriminación de un ítem en el instrumento. Un ítem puede ser adecuado cognitivamente, pero no diferenciar (por ser demasiado fácil) los estudiantes que tienen un mayor o menor conocimiento del concepto. El índice de discriminación encontrado hacia referencia que el los ítems poseen una buena correlación lo que indica que los estudiantes alcanzaron buenas puntuaciones. Esta idoneidad es un componente de la idoneidad instruccional en cuanto que uno de los objetivos de la instrucción es la función evaluadora (Godino, 2011).
• La idoneidad evaluadora también se explica en términos de la fiabilidad de los ítems ya que la fiabilidad determina la medida de estabilidad del instrumento en cuanto al significado de objeto de la evaluación. Los resultados del análisis de fiabilidad del instrumento alfa-theta-omega revelan que el instrumento en general es confiable para evaluar los procesos de resolución de problemas matemáticos en un contexto algebraico.
• La idoneidad afectiva se define con el grado de implicación (ansiedad, agrado, utilidad, motivación, confianza) de los estudiantes en el proceso de resolución de problemas matemáticos. La idoneidad afectiva se refleja en el análisis de las puntuaciones totales. Donde hombres y mujeres que provienen de las especialidades en Informática Administrativa e Ingeniería Agroforestal parecen tener el mismo dominio de los procesos matemáticos para resolver situaciones-problemas en un contexto algebraico.
• La idoneidad epistémica se refleja en la validez del contenido del instrumento, es decir, es el grado de representatividad del instrumento en cuanto al significado objeto de la evaluación. Los resultados de validez de contenido sitúan una buena relación de los contenidos evaluados con los procesos matemáticos que se exteriorizan en contextos algebraicos.
• La idoneidad mediacional es el grado de disponibilidad y adecuación de los recursos materiales y temporales necesarios para el desarrollo del proceso de enseñanza-aprendizaje. En nuestro caso, se refleja en la validez de constructo donde se configura los procesos matemáticos en términos de niveles de complejidad en la resolución de problemas en contexto algebraico.
• La idoneidad ecológica se explica en la validez de contenido, es decir, el grado en que el instrumento se ajusta al contexto del álgebra en que los estudiantes se desarrollan.
En definitiva, la interrelación de las distintas facetas que intervienen en el diseño, implementación y evaluación de procesos matemáticos se explica, primer lugar, en términos de la faceta epistémica y ecológica que generan un sistemas de indicadores asociados a la teoría curricular; en segundo lugar, las facetas cognitiva-afectiva constituyen una teoría de aprendizaje de los procesos matemáticos, y finalmente, las facetas interaccional y mediacional contienen, a su vez, el germen de una teoría de la enseñanza. Partiendo de esto, contestamos la premisa de que un instrumento de evaluación tiene como finalidad proporcionar información sobre los significados personales de un grupo de estudiantes sobre un objeto o un grupo de objetos matemáticos dados.
VI. Lista de referencia
Alsina, A. (2004). Desarrollo de competencias matemáticas con recursos lúdicos-manipulativos. Madrid: Narcea.
Bisquerra, R. (2009). Metodología de la Investigación Educativa. Madrid: La Muralla.
Barbero, M. (2003). Psicometría II. Métodos de elaboración de escalas. Madrid: UNED.
Batanero, C., & Díaz, C. (2003). Análisis de Construcción de un cuestionario sobre probabilidad condicional. Reflexiones desde el marco de las Teoría de las Funciones Semióticas. En C., Batanero, A., Contreras, I., Ordoñez (Eds.): Congreso Internacional sobre las aplicaciones y desarrollo de la teoría de las funciones semióticas, España: Universidad de Jaén.
Batanero, C., & Díaz, C. (2006). Análisis del proceso de construcción de un cuestionario sobre probabilidad condicional. Educación Matemática, Vol. 8, Nº2, 197-223.
Carmines, E., G. & Zeller, R., A. (1979). Reliability and validity assesment. Sage University Paper.
Castro, C., Molina, E., Gutiérrez, M., Martínez, S., & Escorial, B. (2012). Resolución de problemas para el desarrollo de la competencia matemática en educación infantil. Números: Revista de didáctica de las matemáticas, Vol. 80, 53-70.
Dunn, O., J., & Clarck, V., A. (1987). Applied statistics: Analysis of variance and regression. New York: John Wiley.
Frege, G. (1996). Escritos filosóficos. Barcelona: Critica.
Gill, J. (2011). Técnicas e instrumentos para la recogida de información. Madrid: UNED.
Godino, J. (2003). Teoría de las Funciones Semióticas. Un enfoque ontológico y semiótico de la cognición e instrucción matemática. Granada: Universidad de Granada.
Godino, J. (2011). Indicadores de idoneidad didáctica de procesos de enseñanza y aprendizaje de las matemáticas. En XIII Conferencia Interamericana de Educación Matemáticas, Recife: CIAEM-IACME.
Godino, J., Contreras, A., & Roa, R. (2005). An onto-semiotic analysis of combinatorial problems and the solving processes by University students. Educational Studies in Mathematics, Vol. 60, N.1, 3-36.
Hernández, R., Fernández, C., & Baptista, M. (2010). Metodología de la Investigación. México: McGra-Hill.
Heise, D., R., & Bohrnstedt, G., W. (1970). Validity, invalidity, and reliability. In E.E. Borgata & G. W. Bohrnstedt (Eds.), Sociological metholodoly (104-129). San Francisco: Jossey-Bass.
Muñiz, j. (1994). Teoría clásica de los test. Madrid: Pirámide.
Niss, M. (2002). Mathematical competencies and the learning of mathematics. The Danish KOM Project, Denmark, IMFUFA, Roskilde, University.
NCTM. (2000). Principales estándares para la educación matemática. Reston, VA: NCTM.
OECD. (2004). Learning for Tomorrow’s World: First results from PISA 2003. Paris: OECD.
OECD. (2005). Informe PISA 2003. Aprender para el mundo de mañana. Madrid: Santillana.
Pajarez, R., Sanz, A., & Rico, L. (2004). Aproximación a un modelo de evaluación: el proyecto PISA 2000. Madrid: Ministerio de Educación, Cultura y Deporte.
Rico, L. (1997). Organizadores del currículo de matemáticas. En L. Rico (Eds.). La educación matemática en la enseñanza secundaria. Barcelona: Horsori.
Rico, L. (2006). Marco teórico de evaluación en PISA sobre matemáticas y resolución de problemas. Revista de Educación Matemática, extradordinario, 275-294.
Skemp, R. (1976). Relational understanding and instrumental understanding. Mathematics Teaching.
Silbey, R. (2003). Math out loud! Instructor. Vol.112, 7, 24-26.
TIMSS. (2003). Marcos teóricos y especificaciones de evaluación de TIMSS 2003. Madrid: Ministerio de Educación, Cultura y Deporte-INCE.
Tobón, S. (2007). Formación basada en competencias. Pensamiento complejo, diseño curricular y didáctica. Colombia: Ecoe Ediciones.
1 Máster en Investigación en Didácticas de las Ciencias Experimentales y Matemática. Gestor de Proyectos de la Universidad de las Regiones Autónomas de la Costa Caribe Nicaragüense, correo: william.flores@uraccan.edu.ni.
2 Doctora en Psicología. Vicerrectora de Ordenación Académica, Innovación Docente y Calidad de la Universidad de Deusto, España, correo: elena.auzmendi@deusto.es
