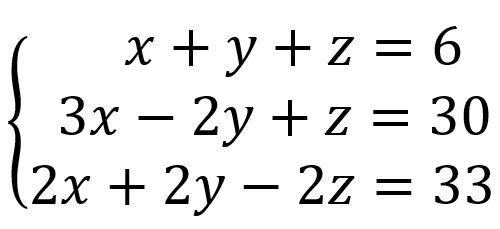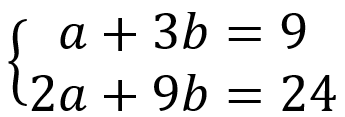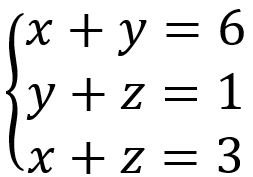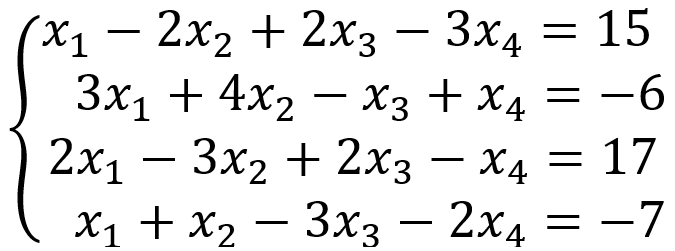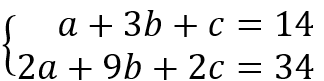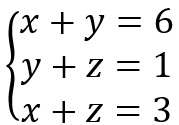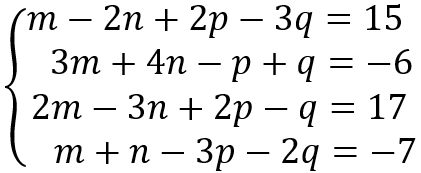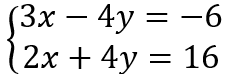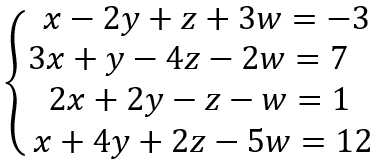Análisis didáctico de Sistemas de Ecuaciones Lineales: Dominios de conocimientos de un profesor de matemática
Didactic analysis of linear equation systems: A math teacher’s areas of expertise
Primitivo Herrera Herrera
Universidad Nacional Autónoma de Nicaragua, Managua. UNAN-Managua, Nicaragua
https://orcid.org/0009-0009-8839-1117
primitivo_herrera@yahoo.com
Osmar Antonio Arias Pérez
Universidad Nacional Autónoma de Nicaragua, Managua. UNAN-Managua, Nicaragua
https://orcid.org/0009-0000-6998-1394
osmararias1002x@gmail.com
RECIBIDO
30/11/2024
ACEPTADO
30/06/2025
RESUMEN
Desde la perspectiva docente, la matemática es una de las disciplinas que presenta diversas dificultades para ser comprendida, a pesar del pleno conocimiento que los docentes tienen del contenido a desarrollar. En estas situaciones, el análisis didáctico juega un rol crucial al facilitar una metodología de investigación que permite escudriñar profundamente un contenido, lo cual ayuda al docente a la planificación, considerando todos los posibles escenarios en una clase. Por ello, el objetivo de este estudio es exponer la utilidad del análisis didáctico para los docentes en formación, enfocado en la temática de Sistemas de Ecuaciones Lineales tomando como referencia su tratamiento en Educación Secundaria. Se realizó en el II semestre 2024. Se aplicó análisis documental de los materiales utilizados para desarrollar esta temática: unidad pedagógica, libros de texto, guía del docente y cuaderno de actividades. A partir de estos resultados, se profundizó en los conocimientos que un profesor de matemática debe poseer para proporcionar un aprendizaje significativo, analizando, describiendo y estableciendo los diferentes significados, sistemas de representación y fenómenos que dan sentido a estos contenidos. Además, se declararon expectativas de aprendizaje, limitaciones y oportunidades, elementos claves para la planificación docente.
PALABRAS CLAVE
Análisis didáctico; sistemas de ecuaciones; planificación; conocimiento didáctico y algebraico.
ABSTRACT
From a teaching perspective, mathematics is one of the disciplines that presents various difficulties in terms of comprehension, despite teachers’ thorough knowledge of the content to be taught. In these situations, didactic analysis plays a crucial role by providing a research methodology that allows for in-depth scrutiny of content, which helps teachers plan, considering all possible scenarios in a class. Therefore, the objective of this study is to demonstrate the usefulness of didactic analysis for teachers in training, focusing on the subject of Linear Equation Systems, taking as a reference its treatment in Secondary Education. It was carried out in the second semester of 2024. A documentary analysis was applied to the materials used to develop this topic: teaching unit, textbooks, teacher’s guide, and activity book. Based on these results, the knowledge that a mathematics teacher must possess to provide meaningful learning was explored in depth, analyzing, describing, and establishing the different meanings, representation systems, and phenomena that give meaning to this content. In addition, learning expectations, limitations, and opportunities were identified as key elements for teaching planning.
KEYWORDS
Didactic analysis; systems of equations; planning; didactic and algebraic knowledge.
INTRODUCCIÓN
El enfoque curricular en Educación General Básica y Media nicaragüense, está definido por competencias, considerando a la persona como sujeto social que tiene las capacidades para realizar múltiples tareas, según las implicaciones cognitivas, comunicativas, motivacionales, volitivas y contextuales. En este sentido, la matemática como ciencia proporciona a los estudiantes una visión más clara y precisa sobre temas que requieren de análisis y de modelización matemática que beneficia la vida social y académica.
Sin embargo, el aprendizaje de la matemática se ve afectado por un sin número de retos, entre ellos está el de transmitir el significado científicamente prioritario de un concepto matemático (Rico et al, 2016), y que, en esencia, se supera con el tratamiento adecuado de los conceptos matemáticos que implica una selección o adaptación idónea de tareas escolares. Es aquí donde entra en juego el análisis didáctico, una metodología de investigación que incluye cuatro categorías: de contenido, cognitivo, instructivo y de actuación; y su función es trascendental para fundamentar, dirigir y sistematizar la planificación, implementación y evaluación de los aprendizajes (Rico et al, 2013).
Por otra parte, la implementación del análisis didáctico en la comunidad educativa para profundizar en contenidos matemáticos específicos ha sido esmerada, tal es el caso de Sáez (2018), que se enfocó en realizar un análisis didáctico sobre el tema de ecuaciones de primer grado y que posterior al análisis, elaboró una unidad didáctica; por su parte, Navas et al (2009), realizó un análisis didáctico sobre el tema de ecuaciones y sistemas de ecuaciones de primer grado, y que finalizó en una propuesta y evaluación de una unidad didáctica. De igual manera, Ortega y Lupiáñez (2012) realizaron una unidad didáctica, así como su evaluación, a partir de un análisis didáctico sobre ecuaciones de primer grado.
Por su parte, el Ministerio de Educación (MINED) aborda el estudio de la matemática en secundaria por medio de los materiales elaborados por el Proyecto de Aprendizaje Amigable de la Matemática en Educación Secundaria (NICAMATE). Esto, a través de libros de textos, los cuales presentan los contenidos de acuerdo a cuatro momentos esenciales: Problema, Solución, Conclusión y Ejercitación; cuadernos de actividades, donde se proponen una serie de tareas para que el estudiante aplique y profundice lo aprendido en el aula. Por último, las guía para docentes brindan una serie de elementos a considerar para la planificación de los contenidos, como son los aprendizajes esperados, la secuencia didáctica, los puntos esenciales y ejemplos de plan de pizarra.
El tratamiento de la unidad de Sistemas de Ecuaciones de Primer Grado en dichos materiales se desarrollan de manera secuenciada, partiendo de conocimientos básicos; como el concepto y solución de una ecuación con una variable, proponiendo tareas enfocadas en resolver ecuaciones mediante la transposición de términos. Seguidamente, se abordan las ecuaciones con dos variables a través de tareas en las que se deben modelar situaciones y utilizar tablas de valores para inducir el concepto de solución de una ecuación de este tipo. Luego, se presenta de forma inductiva el concepto y solución de un sistema de ecuaciones partiendo de tablas de valores que corresponden a dos ecuaciones dadas para lograr establecer una solución común, si existe.
Posteriormente, se muestran los métodos de resolución: sustitución y reducción, el primero se desarrolla mediante tareas en las que se proponen sistemas con una variable despejada y sistemas en las que debe despejarse una de las variables; y el segundo se estudia detalladamente, iniciando a resolver sistemas que tienen una variable con coeficientes opuestos. Después, aquellos en los cuales una variable tiene coeficientes iguales, luego aquellos donde en una de las ecuaciones una de las variables tiene como coeficiente 1 o -1, y, por ende, llegar a resolver sistemas en general.
Finalmente, la aplicación de estos métodos se refleja en sistemas de ecuaciones con paréntesis, fracciones y decimales: así como en la resolución de situaciones geométricas y de la vida cotidiana. De esta manera, se revela la complejidad del trabajo de planificación y las relaciones existentes entre los aspectos disciplinares y didácticos de los contenidos, lo cual se pone de manifiesto en las reflexiones finales de los docentes (Valenzuela et al., 2018).
No obstante, estos documentos carecen de indicaciones concretas que guíen el actuar docente ante las posibles reacciones de los estudiantes, así como de descripciones de posibles dificultades y errores que puedan surgir durante su proceso de aprendizaje en el desarrollo de cada tarea. Por otra parte, el currículo nicaragüense comprende una amplia variedad de temas en cuanto al estudio del álgebra, cuya introducción tiene lugar en séptimo grado, mediante el abordaje de conceptos, notaciones y operaciones básicas, y se extiende por los grados posteriores hasta undécimo grado, culminando en el estudio de las sucesiones aritméticas al calcular y , a partir de los términos conocidos.
Ante la ausencia de indicaciones claras para el actuar docente, así como de las posibles dificultades y errores, y considerando la extensión del álgebra en prácticamente toda la secundaria, surge la necesidad de explorar el contenido matemático y didáctico que deben tenerse en cuenta para el aprendizaje del álgebra. Debido a la riqueza de los contenidos de esta área, los sistemas de ecuaciones presentan una notable complejidad por las múltiples conexiones que establecen con otras ramas de la matemática. Esto sugiere un análisis amplio y completo para poder entender el trasfondo científico, ya que, según Arce Sánchez, Cornejo Garrote y Muñoz Escolano (2019), los saberes de un profesor de matemática deben aglutinar los saberes de diferente naturaleza, lo cual permite que el docente sea consciente de las múltiples dimensiones que posee el conocimiento necesario para enseñar matemática.
Por lo tanto, el estudio se centra en exponer un análisis didáctico de la unidad de sistemas de ecuaciones de primer grado, para escudriñar el contenido desde una perspectiva tanto matemática como didáctica, puesto que en educación secundaria la temática tiene una correspondencia de forma natural entre el álgebra y la geometría. Es decir, el estudiante se encuentra con los entes matemáticos desde dos puntos de vista diferentes, lo que representa un reto para el docente si no tiene el pleno conocimiento de los objetos matemáticos implicados ni de la transición entre sus diversas representaciones.
MATERIALES Y MÉTODOS
El presente estudio, según su enfoque es cualitativo, porque se pretende profundizar, a través de una descripción densa y registro cuidadoso, el contenido de los materiales utilizados por el MINED para impartir los contenidos de sistemas de ecuaciones, con el fin de obtener una coherencia lógica durante el suceso de los hechos (Cortez y León, 2004). En cuanto a su nivel, es descriptiva, porque trata de especificar las propiedades, las características y los perfiles de objetos (en este caso de los materiales: unidad pedagógica, libro de texto, guía docente y cuaderno de actividades de matemática de octavo grado del MINED en el abordaje de sistemas de ecuaciones) que se someta a un análisis, es decir, pretende medir o recoger información de manera independiente o conjunta sobre los conceptos o las variables a las que se refieren (Hernández, Fernández y Baptista, 2010).
Obtenidos los documentos curriculares de dominio público y utilizados únicamente con fines académicos respetando la fuente institucional del Ministerio de Educación, se procedió a realizar la revisión de cada uno de ellos, centrándose en la unidad II: Sistemas de ecuaciones de primer grado de octavo grado de Educación Secundaria. Esa información se analizó llevando a cabo el Análisis Didáctico propuesto por Rico (2016), el cual se estructura en cuatro tipos de análisis: contenido, cognitivo, instructivo y de actuación, cada uno vinculado con una dimensión del currículo: cultural-conceptual, cognitiva, ético-normativa y social, respectivamente.
Las categorías que caracterizan cada tipo de análisis son las siguientes:
- Para el análisis de contenido: estructura conceptual, sistemas de representación y sentidos y modos de uso.
- Para el análisis cognitivo: expectativas y limitaciones en el aprendizaje.
- Para el análisis instructivo: tareas, secuencias, organización, materiales y recursos.
- Para el análisis de actuación: modalidades, diseño, intervención y evaluación.
Este estudio se centra en los tres primeros tipos de análisis, ya que permiten sintetizar la significatividad, estructura y organización de los contenidos matemáticos.
Como instrumento para el análisis documental se utilizó una adaptación del registro de observación expuesto por González y Gallarda (2013), considerando los aspectos que caracterizan a cada categoría y que son expuestos en la siguiente tabla:
| Análisis de contenido | Análisis cognitivo | Análisis instruccional |
|---|---|---|
Campo conceptual:
Campo procedimental:
Campo actitudinal:
Sistemas de representación. Fenomenología. Estructura de la unidad. |
Expectativas declaradas para los contenidos de la unidad (descripción de las competencias, indicadores de logro y aprendizajes esperados). Limitaciones declaradas para los contenidos (descripción de los errores y dificultades) |
Metodología:
Roles en el aula:
Tareas. Aquí se selecciona:
Recursos y materiales sugeridos. |
RESULTADOS Y DISCUSIÓN
En este apartado se presenta el análisis didáctico de la temática de sistemas de ecuaciones atendiendo al análisis de contenido, seguido del cognitivo y, por último, el instructivo.
- Análisis de contenido
Campo conceptual
| Términos Ecuación, solución, incógnita, coeficientes, términos independientes. |
Conceptos
|
Estructura: Espacio vectorial y . |
Notaciones: Ecuación de primer grado en dos variables:
Solución de este tipo de ecuaciones: Otras han sido particularizadas a los objetos tratados como:
|
Relaciones:
|
Convenios
|
|
Resultados
|
|
Campo procedimental
Destrezas:
|
Razonamiento: Figurativo: al encontrar las soluciones de un sistema de ecuaciones de la intersección de rectas asociados a las ecuaciones del sistema. |
Estrategias:
|
Campo actitudinal
Emociones:
|
|
Moralidad y normas:
|
Valores éticos:
|
Este análisis manifiesta que el profesor de matemáticas que aborda el contenido de sistemas de ecuaciones debe ser, ante todo, un mediador consciente entre el saber formal y la experiencia del aprendizaje significativo. El campo conceptual refleja que este debe comprender con profundidad las estructuras algebraicas y geométricas que lo sustenta y la naturaleza de sus soluciones desde una perspectiva analítica y gráfica. Esto le permite anticipar dificultades conceptuales y ofrecer explicaciones claras, rigurosas y contextualizadas.
En cuanto a lo procedimental, el docente necesita interpretar los procesos de pensamiento de sus estudiantes, reconociendo cuándo se activan razonamientos figurativos o deductivos, y cómo potenciar la selección estratégica de los métodos de resolución. Esta comprensión le permite dosificar la enseñanza, proponer tareas desafiantes y promover el tránsito entre distintos registros de representación.
Por último, en el ámbito actitudinal, el docente guía la actitud hacia las matemáticas. Fomenta la apreciación por el orden lógico, el valor de una solución coherente, y la autorregulación en la resolución de problemas. Además, modela el valor de la honestidad intelectual, la perseverancia y el respeto por las normas del pensamiento matemático.
En síntesis, un docente competente en estos tres campos transforma el estudio de los sistemas de ecuaciones en una experiencia formativa integral, en la que se cultivan el pensamiento crítico, la autonomía intelectual y el compromiso ético con el conocimiento; a través de los siguientes focos conceptuales:
- Caracterización de los sistemas de ecuaciones lineales. Involucra la definición y clasificación de los sistemas de ecuaciones lineales: compatible determinado, compatible indeterminado, incompatibles.
- Métodos de resolución de los sistemas de ecuaciones lineales. Incorpora el conocimiento de los métodos que facilitan la resolución de un sistema de ecuaciones lineales: método de sustitución y eliminación.
- Aplicaciones de los sistemas de ecuaciones lineales. Toma en consideración los sistemas de ecuaciones lineales para la resolución de problemas de programación, agricultura, física, ingeniería, química y economía.
Sistemas de representación
En los sistemas de representación en matemática usualmente se distinguen dos familias de representaciones: las simbólicas y las gráficas. Al respecto, Rico et al. (2016) explican que:
Las simbólicas incluyen símbolos alfanuméricos que se emplean con unas reglas de procedimiento. Las representaciones gráficas son de tipo figurativo y también disponen de unas reglas de composición y de unos convenios de interpretación. A partir de estas dos familias, y dependiendo del concepto que se trabaje, surgen otros sistemas de representación que expresan facetas de ese concepto. (p.120)
En este sentido, dentro de la temática de interés es priorizada la representación simbólica, que contiene las combinaciones de símbolos y números que corresponden al concepto de sistemas de ecuaciones lineales. Ejemplificados de la siguiente manera:
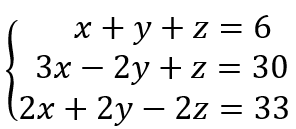
En lo que respecta a la representación gráfica de sistemas 2×2, aunque no se aborda de manera explícita, el docente puede profundizar en su comprensión vinculándola con las representaciones de ecuaciones lineales en dos variables trabajadas en séptimo grado, lo que le permite establecer los siguientes casos:
Dos rectas concurrentes en ![]() . (El sistema admite una única solución)
. (El sistema admite una única solución)
Dos rectas paralelas (El sistema no admite solución).
Dos rectas coincidentes (El sistema admite infinitas soluciones).
Figura 1: Representación geométrica de sistemas .
Representación verbal, la cual consiste en la transcripción del lenguaje común a la representación simbólica. Por ejemplo:
El doble de la edad de Luis más la edad de Carlos es 11 años. Si Carlos es dos años mayor que Luis, encuentre las edades de Luis y Carlos respectivamente.
Transcribir este problema al lenguaje simbólico consiste en tomar las edades de Luis y Carlos como incógnitas y etiquetarlas respectivamente como y luego, por los datos del problema, se construye el sistema lineal 2 X 2:
cuya solución es (3,5). Esto quiere decir que la edad de Luis es 3 y la de Carlos es 5.
Un tratamiento similar se hace para sistemas de ecuaciones lineales 3x3, aunque estos se presentan como contenidos de tipo “desafío”, resolviéndose mediante el método de reducción. Su abordaje se plantea con un mayor nivel de complejidad, y se sugiere que su inclusión en el aula dependerá de la disponibilidad de tiempo y de las características del grupo de estudiantes.
En términos generales, las representaciones predominantes en los materiales analizados son la simbólica y la verbal, lo que evidencia una orientación hacia un enfoque principalmente algebraico. Esta perspectiva deja de lado la interpretación geométrica de las ecuaciones, la cual resulta fundamental para que los estudiantes comprendan la naturaleza de las soluciones de un sistema de ecuaciones lineales.
Fenomenología
A pesar de que en los materiales analizados no abordan explícitamente el origen de los conceptos matemáticos tratados, es fundamental que el profesor de matemática reconozca cómo estos han sido históricamente construidos y desarrollados. Esta perspectiva no solo contribuye a humanizar el aprendizaje, sino que también promueve el reconocimiento de la diversidad de aportes culturales en la evolución del pensamiento matemático.
Al respecto se puede señalar que: los babilonios (2000 a.C. – 600 a.C.) utilizaban tabillas de arcilla donde registraban sus problemas que trataban situaciones de comercio herencia, división de propiedades, etc. Ellos también estudiaron problemas que involucraban ecuaciones lineales simultáneas y el método que utilizaban para resolver dichos problemas era similar a lo que hoy conocemos como el método de eliminación. A diferencia de la notación que hoy conocemos, en lugar de incógnitas, utilizaban palabras como longitud, anchura, volumen, área; a pesar de no relacionarse con problemas de medidas.
Los egipcios (2000 a.C. – 1800 a.C.), por su parte, planteaban problemas donde estaba inmerso el concepto de ecuación lineal. Estos problemas daban lugar a ecuaciones del tipo x + ax = b o x + ax + bx = c, donde a, b y c son números conocidos y x es el número desconocido. El método que utilizaban los egipcios consistía en asignar un valor al azar a la incógnita para luego realizar las cuentas, obtener el resultado y posteriormente utilizar las proporciones para así llegar a la respuesta correcta.
De la misma manera, los chinos (200 a.C. – 100 a.C.) trataban problemas que involucraban ecuaciones lineales, y los métodos que ellos emplearon eran similares a lo que hoy conocemos como Método de Eliminación Gaussiana y fue utilizado antes que se tuvieran las representaciones de las ecuaciones o variables.
Otro aspecto que contempla la fenomenología son las situaciones, que para Rico et al. (2016) “el marco del estudio PISA considera cuatro tipos de situaciones para analizar y categorizar las tareas que se incluyen en las pruebas de evaluación. Estas categorías organizan las situaciones que se consideran: Personales, laborales, sociales, científicas.” (p. 146).
En este sentido, dentro de los materiales analizados, las situaciones que abordan sistemas de ecuaciones lineales se centran en contextos personales, como problemas relacionados con la edad o la compra de productos, a manera de ejemplos ilustrativos:
a. Erick es 2 años menor que Lucia. Si la suma de ambas edades es 28, ¿cuál es la edad de cada uno de ellos? b. Por la compra de dos pantalones y tres camisas se pagan C$ 1 200. Sabiendo que el costo de un pantalón excede en C$ 100 al de una camisa, ¿cuál es el costo de cada artículo?
Además, hacen referencia a aplicaciones geométricas que pueden ser consideradas como situaciones científicas, entre ellas: En un rectángulo cuyo perímetro es 70 cm, el doble de la base excede en 20 cm al triple de la altura. ¿Cuáles son las medidas de la base y la altura?
Los contenidos de sistemas de ecuaciones se ven transversalizados en otras áreas como:
- Situaciones laborales: Si la economía de una nación se divide por sectores: carbón, electricidad y acero. Por ejemplo, la producción total de electricidad se divide como sigue: un 40% (0.4) de carbón, un 50% (0.5) de acero, y el restante 10% (0.1) de electricidad. (El sector eléctrico trata este 10% como un gasto en que incurre para hacer funcionar su negocio.) Los precios (es decir, valores en moneda) de la producción total de los sectores de carbón, electricidad y acero se denotarán como , y , respectivamente. Si quisiéramos encontrar los precios de equilibrio que permiten a los ingresos de cada sector igualar sus gastos; entonces de acá surge un sistema homogéneo:
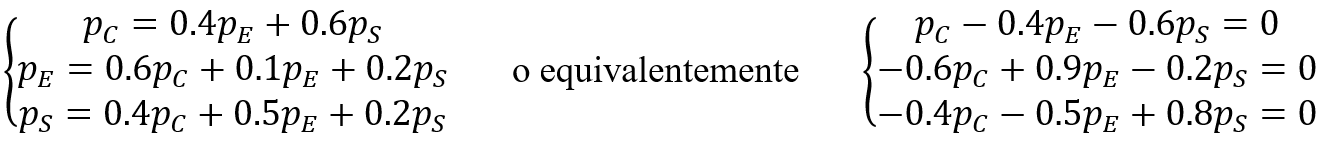
- Situaciones sociales: La aplicación de los sistemas lineales también se da en el flujo de tráfico. Se tiene una red de caminos de un solo sentido en forma rectangular, la cual se muestra en la figura de abajo. Los números representan la cantidad de vehículos por hora que entran o salen por cada nodo. Por cada camino de la red se tiene una variable, y cada camino tiene su dirección representada por una flecha (Figura 2).
Si se quiere, por ejemplo, controlar la cantidad de vehículos que entra y sale en cada nodo, a partir de este diagrama, podemos modelar el problema con un sistema de ecuaciones lineales. Primero obtenemos una ecuación por cada nodo, tomando las entradas y salidas de vehículos:
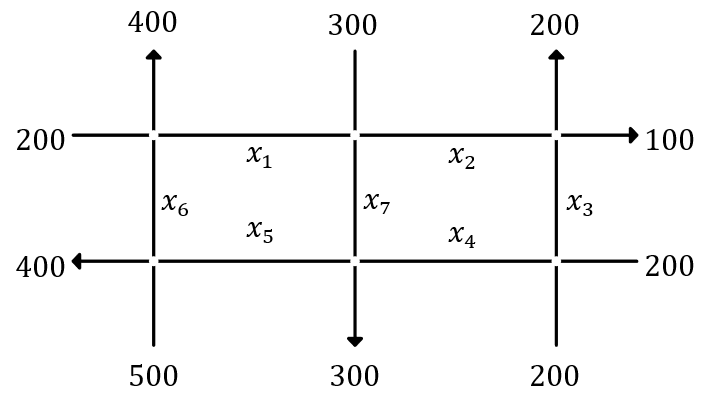
Figura 2: Red de tráfico.
Si se quiere, por ejemplo, controlar la cantidad de vehículos que entra y sale en cada nodo, a partir de este diagrama, podemos modelar el problema con un sistema de ecuaciones lineales. Primero obtenemos una ecuación por cada nodo, tomando las entradas y salidas de vehículos:

- Situaciones científicas: Otra aplicación de los Sistemas Lineales se sumerge en la Química, como por ejemplo el balanceo de ecuaciones químicas. Un caso más específico es, que al quemar gas propano (), este se combina con oxígeno () para formar dióxido de carbono () y agua (), de acuerdo con una ecuación de la forma
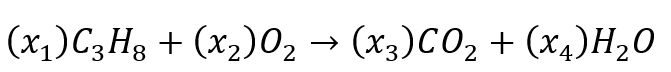
y para balancear esta ecuación, un químico debe encontrar números enteros x1,...,x4 tales que el número total de átomos de carbono (C), hidrógeno (H) y oxígeno (O) situados a la izquierda sea igual al número correspondiente de átomos ubicados a la derecha. Al plantear las ecuaciones correspondientes, se obtiene el siguiente sistema.
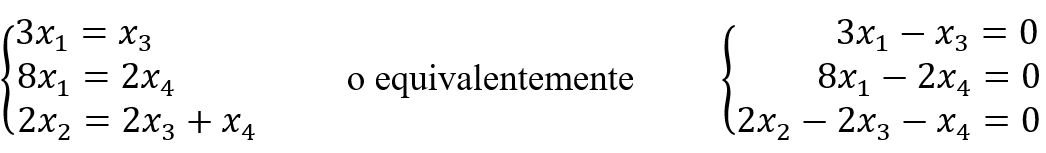
Por tanto, reconocer la diversidad de contextos en los que se aplican los sistemas de ecuaciones permite al docente conectar el conocimiento abstracto con situaciones reales, favoreciendo una enseñanza más significativa y funcional.
- Análisis cognitivo
Expectativas y competencias
En lo que respecta a esta subcategoría, se evidencia una coherente articulación entre niveles de concreción educativa, que asegura que el desarrollo de competencias matemáticas ocurra con sentido, progresividad y aplicabilidad.
Con respecto a las competencias de la asignatura, estas expresan una visión holística de la matemática como herramienta de transformación personal y social, destacando:
- El uso del conocimiento científico-tecnológico para transformar realidades.
- El razonamiento lógico-crítico y filosófico, como base de la solución de problemas complejos.
- La comprensión y representación gráfica de situaciones, esenciales para conectar lo abstracto con lo visual.
- La autoformación mediante estrategias y modelos, promoviendo autonomía en el aprendizaje.
Por su parte, la competencia de grado profundiza esta perspectiva en el eje de sistemas de ecuaciones lineales, priorizando la resolución de problemas contextualizados que requieren formular, modelar y resolver sistemas de dos y tres variables. Esto se traduce en aprendizajes esperados precisos: desde el dominio de técnicas algebraicas básicas (transposición de términos), hasta la aplicación de métodos de sustitución y reducción en diversas situaciones estructurales (coeficientes fraccionarios, decimales o con paréntesis), culminando en la aplicación a problemas reales o geométricos.
A pesar de lo previamente señalado, no se explicita una correspondencia directa entre los aprendizajes esperados y las competencias matemáticas específicas definidas en el marco de referencia PISA 2012 —razonar y argumentar (RA), comunicar (C), matematizar (M), elaborar estrategias para resolver problemas (RP), representar (R), utilizar lenguaje simbólico, formal y técnico (LS) y emplear herramientas matemáticas (HM)—. Esta ausencia motivó la reformulación de dichos aprendizajes en forma de objetivos específicos, alineados con los focos conceptuales identificados, con el fin de establecer vínculos claros y operativos entre lo que se enseña y las habilidades clave que deben desarrollar los estudiantes.
| Objetivos específicos | RA | C | M | RP | R | LS | HM | |
|---|---|---|---|---|---|---|---|---|
| Foco 1: Caracterización de los sistemas de ecuaciones lineales | ||||||||
| O1. | Definir el concepto y clasificación de sistemas de ecuaciones lineales. | X | X | |||||
| O2. | Identificar soluciones de un sistema de ecuaciones. | X | X | X | ||||
| Foco 2: Métodos de resolución de los sistemas de ecuaciones lineales | ||||||||
| O3. | X | X | X | X | ||||
| O4. | Resolver sistemas de ecuaciones lineales haciendo uso de GeoGebra. | X | X | X | ||||
| Foco 3: Aplicaciones de los sistemas de ecuaciones lineales | ||||||||
| O5. | Resolver problemas de enunciado verbal haciendo uso de los sistemas de ecuaciones lineales. | X | X | X | X | X | X | |
Dificultades y errores
Los materiales analizados no hacen alusión explícita a posibles limitaciones en el aprendizaje de los contenidos abordados. No obstante, a partir de los análisis realizados, es posible anticipar dificultades y errores que los estudiantes podrían enfrentar durante el estudio de los sistemas de ecuaciones lineales, así como identificar los objetivos específicos cuya formulación podría obstaculizar el aprendizaje. De acuerdo con Gamboa, Castillo e Hidalgo (2018), los errores se entienden como prácticas —acciones, argumentaciones, entre otras— que no son válidas desde el punto de vista de la institución matemática escolar, mientras que las dificultades, en términos simples, corresponden a las causas o condiciones que dan origen a dichos errores.
| Dificultades y errores | Objetivos asociados | |
|---|---|---|
| D1. | Dificultades asociadas a la comprensión conceptual | |
| E1. | Prescindir el orden de las componentes al comprobar la solución de un sistema de ecuaciones lineales. | O2 |
| E2. | Interpretar como una misma incógnita a incógnitas diferentes de una ecuación. | O1, O2 |
| E3. | Confundir el número de ecuaciones por el número de incógnitas o viceversa. | O1, O2, O3 |
| D2. | Dificultades asociadas a la realización de cálculos | |
| E4. | Realizar operaciones en un solo miembro de la igualdad al momento de reescribir una ecuación equivalente. | O3, O4, O5 |
| E5. | Sumar incorrectamente números de diferentes signos. | O2, O3 |
| E6. | Aplicación incorrecta de la ley de los signos. | O2, O3 |
| E7. | Realizar cálculos con operaciones combinadas sin respetar la jerarquía de operaciones. | O2, O3 |
| E8. | Sustituir la incógnita en la misma ecuación en la que se despejó. | O3, O5 |
| E9. | Fallar al realizar operaciones algebraicas al despejar una incógnita. | O3, O5 |
E10. |
Utilizar la misma incógnita para representar diferentes cantidades. | O5 |
| D3. | Dificultades asociadas a la modelización matemática | |
| E11. | Considerar la intersección manual de los objetos que representan las ecuaciones como solución del sistema al usar la graficadora de GeoGebra. | O4, O5 |
| E12. | Omitir las comas como separador de las ecuaciones al momento de utilizar la herramienta resuelve de GeoGebra. | O4, O5 |
E13. |
Resolver el sistema sin antes ordenar las ecuaciones. | O2, O3, O4 |
| E14. | Traducir de manera errónea condiciones dadas en el problema. | O5 |
| E15. | Prescindir de la interpretación de la solución de un sistema como respuesta del problema planteado. | O5 |
Estos errores evidencian la necesidad de que el docente asuma una actitud reflexiva al momento de planificar sus clases, considerando de forma anticipada los posibles escenarios que podrían surgir en el aula. Esta previsión contribuye a brindar mayor claridad y certeza frente a las reacciones del estudiantado. Asimismo, cada intervención del profesorado puede orientarse estratégicamente en función de los objetivos específicos de la clase, fortaleciendo la toma de decisiones pedagógicas con intencionalidad didáctica.
- Análisis instructivo
En lo que respecta a la instrucción, los materiales presentan una metodología secuenciada que incluye problema, solución, conclusión, ejemplo y ejercicios para el libro de texto, aprendizaje esperado, secuencia didáctica, puntos esenciales y plan pizarra en la guía docente; sin embargo, no se especifican los recursos o materiales que podrían emplearse en su implementación, ni se detalla el nivel de alcance y complejidad de las actividades de aprendizaje propuestas.
Como ejemplos ilustrativos integradores, se proponen seis tareas distribuidas según las fases de una clase, centradas en dos contenidos relacionados con los sistemas de ecuaciones lineales: El concepto como tal y la resolución integrando tecnología. Cada tarea detalla los elementos clave a considerar durante su implementación, con el fin de guiar la acción docente de manera reflexiva y estructurada.
Tarea de inicio
| Objetivo de aprendizaje | Identificar el número de incógnitas en una ecuación. | |||||||||||||||
| Recursos y materiales | Lámina de papel en la que se llevará la tabla de la actividad. | |||||||||||||||
| Nivel de alcance y complejidad | Aplicación y reproducción. | |||||||||||||||
| Dificultades y errores asociados | D1: Dificultades asociadas a la comprensión conceptual. E3: Interpretar como una misma incógnita a incógnitas diferentes de una ecuación. |
|||||||||||||||
Situación: Escribe en cada casilla la información solicitada para cada ecuación.
|
||||||||||||||||
Tarea de desarrollo
| Objetivo de aprendizaje | Identificar el tamaño de un sistema dado. | ||||||||||||||||
| Recursos y materiales | Lámina de papel en la que se llevará la tabla de la actividad. | ||||||||||||||||
| Nivel de alcance y complejidad | Aplicación y reproducción. | ||||||||||||||||
| Dificultades y errores asociados | D1: Dificultades asociadas a la comprensión conceptual. E4: Confundir el número de ecuaciones por el número de incógnitas o viceversa. |
||||||||||||||||
Situación: Escribe en cada casilla la información solicitada para cada sistema de ecuaciones lineales.
|
|||||||||||||||||
Tarea de cierre
| Objetivo de aprendizaje | Asociar el tamaño de un sistema con el número de ecuaciones e incógnitas. | ||||||||
| Recursos y materiales | Lámina de papel en la que se llevará la tabla de la actividad. | ||||||||
| Nivel de alcance y complejidad | Aplicación y reproducción. | ||||||||
| Dificultades y errores asociados | D1: Dificultades asociadas a la comprensión conceptual. E3: Interpretar como una misma incógnita a incógnitas diferentes de una ecuación. E4: Confundir el número de ecuaciones por el número de incógnitas o viceversa. |
||||||||
Situación: Escribe en cada casilla la información solicitada para cada ecuación.
|
|||||||||
Considerando la demanda actual de incorporar la tecnología en el proceso de enseñanza-aprendizaje de contenidos matemáticos, se ha dispuesto presentar las siguientes tareas utilizando GeoGebra como recurso que favorece la representación geométrica de cada una de las ecuaciones algebraicas del sistema, así como de la determinación de su conjunto solución.
Tarea de inicio
Objetivo de aprendizaje |
Interpretar geométricamente la compatibilidad e incompatibilidad de sistemas lineales utilizando GeoGebra . |
| Recursos y materiales | Celular o Computador compatibles con la versión de GeoGebra . |
| Nivel de alcance y complejidad | Interpretación y conexión. |
| Dificultades y errores asociados | D3: Dificultades asociadas a la modelización matemática. E11: Considerar la intersección manual de los objetos que representan las ecuaciones como solución del sistema al usar la graficadora de GeoGebra. |
Situación: Grafica las rectas que representan las ecuaciones del sistema a partir de los siguientes pasos:
|
|
Tarea de desarrollo
| Objetivo de aprendizaje | Interpretar geométricamente la compatibilidad e incompatibilidad de sistemas lineales utilizando GeoGebra . |
| Recursos y materiales | Celular o Computador compatibles con la versión de GeoGebra . |
| Nivel de alcance y complejidad | Interpretación y conexión. |
| Dificultades y errores asociados | D3: Dificultades asociadas a la modelización matemática. E11: Considerar la intersección manual de los objetos que representan las ecuaciones como solución del sistema al usar la graficadora de GeoGebra. |
Situación: Resuelve geométricamente el siguiente sistema de ecuaciones:
|
|
Tarea de cierre
| Objetivo de aprendizaje | Resolver sistemas de ecuaciones utilizando herramientas de GeoGebra. |
| Recursos y materiales | Celular o Computador compatibles con la versión de GeoGebra . |
| Nivel de alcance y complejidad | Aplicación y reproducción. |
| Dificultades y errores asociados | D3: Dificultades asociadas a la modelización matemática. E13: Resolver el sistema sin antes ordenar las ecuaciones. |
Situación: Resuelve el siguiente sistema:
|
|
Desde el punto de vista del contenido matemático, las tareas relacionadas con el concepto de sistemas de ecuaciones lineales se centran en reconocer el tamaño de un sistema a partir de la identificación del número de ecuaciones y variables involucradas. Esto facilita la manipulación del concepto y estructura de una ecuación lineal, así como del arreglo rectangular implícito. Por otro lado, las tareas iniciales y de desarrollo propuestas para la resolución de sistemas de ecuaciones lineales utilizando GeoGebra buscan representar geométricamente cada una de las ecuaciones lineales para visualizar sus posiciones relativas y, en consecuencia, determinar el conjunto solución del sistema. Sin embargo, a través de la tarea de cierre, se explora el cálculo simbólico integrado en este software como una herramienta alternativa para resolver sistemas de diferentes tamaños; contribuyendo al desarrollo de las competencias razonar, representar, uso del lenguaje simbólico formal y técnico y utilización de herramientas matemáticas.
En definitiva, diseñar tareas no es una actividad mecánica, sino un acto profesional complejo que revela y exige del docente un saber profundo y reflexivo sobre lo que significa enseñar y aprender matemática.
CONCLUSIONES
El análisis didáctico desarrollado permitió evidenciar que el estudio de los sistemas de ecuaciones lineales, pese a su abordaje puntual en los materiales de secundaria, encierra una notable densidad matemática, histórica y pedagógica. Esta investigación demostró que su tratamiento en el aula exige del profesorado una comprensión profunda de los fundamentos conceptuales, los métodos de resolución, los sistemas de representación y los diversos contextos de aplicación, lo cual habilita procesos de enseñanza más significativos y contextualizados.
Asimismo, el análisis puso de manifiesto la importancia de anticipar errores y dificultades recurrentes en los estudiantes, destacando la necesidad de que el docente adopte una actitud reflexiva y prospectiva al momento de planificar. Esta postura le permite diseñar secuencias didácticas que favorezcan el tránsito entre registros semióticos, el uso intencionado de herramientas tecnológicas como GeoGebra, y el desarrollo de una comprensión más robusta y flexible de los contenidos.
Desde una perspectiva formativa, se concluye que enseñar sistemas de ecuaciones no debe restringirse a la aplicación mecánica de algoritmos, sino orientarse al desarrollo de competencias matemáticas clave: razonar, comunicar, modelar, argumentar y representar. La vinculación de los aprendizajes esperados con las competencias definidas en el marco de referencia PISA 2012 otorga coherencia entre el currículo declarado y las habilidades que los estudiantes requieren para desenvolverse en situaciones reales.
En términos de contribución al conocimiento científico y didáctico del profesorado, este estudio reivindica el valor del análisis didáctico como herramienta de investigación pedagógica y como soporte estratégico para la toma de decisiones en el aula. Su aplicación permite seleccionar contenidos con criterio, prever escenarios posibles, fundamentar metodológicamente la práctica docente y conectar saberes disciplinares con dimensiones éticas, emocionales y cognitivas del aprendizaje.
En definitiva, una enseñanza efectiva de los sistemas de ecuaciones demanda un docente capaz de transitar entre el conocimiento especializado y la práctica situada, que interprete los contenidos desde su densidad matemática, los modele desde una mirada histórica-fenomenológica y los convierta en experiencias significativas que otorguen sentido al conocimiento en la vida del estudiantado.
REFERENCIAS BIBLIOGRÁFICAS
Arce Sanchez, M., Cornejo Garrote, L., & Muñoz Escolano, J. M. (2019). Aprendizaje y enseñanza de las matemáticas. Síntesis.
Cortés, M., & León, M. (2004). Generalidades sobre Metodología de la Investigación . Ciudad del Carmen: Universidad Autónoma del Carmen .
Gamboa, R., Castillo, M., & Hidalgo, R. (2018). Errores matemáticos de estudiantes que ingresan a la universidad. Actualidades Investigativas en Educación, 1-31. https://www.scielo.sa.cr/scielo.php?script=sci_arttext&pid=S1409-47032019000100104
Hernández, R., Fernández , C., & Baptista, M. (2010). Metodología de la investigación . México: Interamericana Editores, S.A de C.V.
Herrera Herrera, P., Rojas Rojas, J. A., Rueda Sánchez, D. A., Muller, E. W., García Acevedo, A. L., Salgado, J. C., . . . Chamorro Domingo, A. (2019). Cuarta unidad pedagógica secundaria regular. Grado: séptimo, octavo y noveno grado. Asignatura: matemática. Managua: MINED.
José Luis González-Mari y Jesús Gallardo. (2013). Análisis didáctico curricular: un procedimiento para fundamentar el diseño, el desarrollo y la evaluación de unidades didácticas de matemáticas. En J. E. Rico, Análisis didáctico en educación matemática. Metodología de investigación, formación de profesores e innovación curricular (págs. 161-190). Editorial Comares.
Matias, Arce Sánchez, M., Conejo Garrote, L., & Muñoz Escolano, J. M. (2019). Aprendizaje y enseñanza de las matemáticas. Madrid: Editorial Síntesis.
Mnisterio de Educación [MINED]. (2022). nicaraguaeduca.mined.gob.ni.
https://nicaraguaeduca.mined.gob.ni/wp-content/uploads/2023/07/II-y-III-UP-Matematica-Primaria-Multigrado-170523-VF.pdf
Navas, Y., Fuentes, V., Ondoño, P., Fernández, J., & Fernández, F. (2009). Unidad didáctica: Ecuaciones de Primer Grado y Sistemas de Ecuaciones. https://funes.uniandes.edu.co/funes-documentos/unidad-didactica-ecuaciones-de-primer-grado-y-sistemas-de-ecuaciones/
Ortega , A., & Lupiáñez, J. (2012). Unidad didáctica: Ecuaciones de Primer Grado. Granada.
https://fqm193.ugr.es/media/grupos/FQM193/cms/TFM_OrtegaTorres.pdf
Rico, L., Lupiáñez , J. L., & Molina, M. (2013). Análisis Didáctico en Educación Secundaria. Granada: Comares, S. L.
Rico, L., Moreno , A., Ruiz , J., Fernández, J., Martínez , P., Lupiáñez, J., . . . Segovia, I. (2016). Elementos de la didáctica de la matemática para el profesor de secundaria. España: Ediciones Pirámide S.A.
Sáez, A. (2018). Unidad diáctica: Sistemas de ecuaciones (2do ESO). Granada.
https://digibug.ugr.es/bitstream/handle/10481/56468/TFM_AlejandroSaezTarifa%20%281%29.pdf?sequence=1&isAllowed=y
Valenzuela, M., Ramos, E., González, L. I., & Portugal, J. L. (2018). El análisis didáctico como base de un curso en la formación inicial de profesores de educación primaria. Revista Iberoamericana de Educación Superior, 118-137. https://www.redalyc.org/journal/2991/299158443007/html/
ANEXOS
REGISTRO DE ANÁLISIS DOCUMENTAL
Con este instrumento se pretende realizar un análisis documental de la unidad pedagógica, libro de texto, guía docente y cuaderno de actividades del área de matemática del Ministerio de Educación, centrado en contenidos, expectativas, limitaciones, organización y oportunidades de aprendizaje declaradas para la Unidad
II: Sistemas de ecuaciones de primer grado de 8vo grado de Educación Secundaria.
I. Análisis de contenido
| Campo conceptual |
|---|
| Hechos Términos Notaciones Convenios Resultados Conceptos Conceptos Relaciones Estructura conceptual |
| Campo procedimental |
| Descripción de: Destrezas que se pretenden desarrollar desde los contenidos de la unidad. Razonamientos que se pueden manifestar: Deductivo Inductivo Analógico Figurativo Estrategias que se pueden utilizar en el desarrollo de los contenidos de la unidad. |
| Campo actitudinal |
| Emociones, normas y valores éticos que se promueven desde los contenidos de la unidad. |
| Sistemas de representación |
|---|
| Utilizados en los contenidos de la unidad: Simbólico: Gráfico: Numérico: Verbal: |
| Fenomenología |
| Datos históricos presentes en los contenidos de la unidad. |
| Tipos de situaciones presentes en los contenidos de la unidad. |
| Estructura de la unidad |
|---|
| Unidad: Sección: Contenidos: |
II. Análisis cognitivo
| Expectativas declaradas para los contenidos de la unidad |
|---|
| Competencias: Indicadores de logros: Aprendizajes esperados: |
| Limitaciones declaradas para los contenidos de la unidad |
| Errores (Advertencias): Dificultades: |
III. Análisis instructivo
| Metodología |
|---|
| Descripción de la metodología sugerida para el desarrollo de los contenidos de la unidad. |
| Actuación docente implícita en la unidad. Guiada Semiguiada Expositiva Transmisiva otros: s Tipos de aprendizaje que pueden ocurrir al trabajar con la unidad. Memorístico Constructivo Comprensivo Descubrimiento Significativo No significativo |
| Roles en el aula |
| Que se recomiendan sean adoptados en la unidad. Profesor: Activo Pasivo Protagonista Guía Controlador Profesional autónomo Profesional dependiente Otros: s Estudiante: Activo Pasivo Protagonista Ejecutor Obediente/sumiso Autónomo Dependiente Otros: |
| Tareas |
| Recomendadas para que las realicen: los estudiantes el profesor ambos Declaradas para las fases de las sesiones de clases: Inicio Desarrollo Cierre Formas de agrupación sugeridas para su desarrollo: Individual Pequeño Grupo Grupo mediano Gran grupo Agrupamiento mixto Nivel de complejidad: Reproducción Conexión Reflexión Mixta: |
| Recursos y materiales didácticos |
| Recursos que son requeridos para el desarrollo de los contenidos de la unidad: Videos Murales Televisión Manualidades Diapositivas Folletos Exposiciones |
Materiales didácticos sugeridos para el desarrollo de los contenidos de la unidad:
|
© 2025 Revista Científica Estelí.
![]() Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.